105 學年度身心障礙學生升學大專校院甄試
甄試類(群)組別:四技二專組-數學(A)
單選題,共 20 題,每題 5 分
解答:$$\cases{A(-4,6)\\ C(4,0)} \Rightarrow \overrightarrow{AC}=(8,-6)\Rightarrow 過B(-2,0)且法向量為\overrightarrow{AC}的直線:8(x+2)-6y=0\\ \Rightarrow 4x-3y=-8,故選\bbox[red,2pt]{(D)}$$
解答:$$\cos(-240^\circ) +\sin 330^\circ\times \tan 945^\circ =\cos 240^\circ+\sin(360^\circ-30^\circ)\times \tan(360^\circ\times 2+225^\circ)\\ =- \cos 60^\circ-\sin 30^\circ\times \tan 225^\circ =-{1\over 2}-{1\over 2}\times 1=-1,故選\bbox[red,2pt]{(C)}$$
解答:$$餘弦定理: \cos \angle A= {\overline{AB}^2+ \overline{AC}^2-\overline{BC}^2\over 2\cdot \overline{AB}\cdot \overline{AC}} \Rightarrow \cos 60^\circ ={3^2+5^2 -\overline{BC}^2\over 2\cdot 3\cdot 5} \Rightarrow {1\over 2}= {34-\overline{BC}^2\over 30} \\ \Rightarrow \overline{BC}^2 =19 \Rightarrow \overline{BC}=\sqrt{19},故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{\vec a=(3,4)\\ \vec b=(2,-1)} \Rightarrow 3\vec a+5\vec b=3(3,4)+5(2,-1) = (9,12) +(10,-5) = (19,7),故選\bbox[red,2pt]{(A)}$$
解答:$$\cases{A(1,2)\\ B(3,1)\\ C(a,b)} \Rightarrow \cases{\overrightarrow{BA}= (-2,1)\\ \overrightarrow{BC} =(a-3,b-1)},又\angle ABC=90^\circ \Rightarrow \overrightarrow{BA}\cdot \overrightarrow{BC}=0 \Rightarrow -2a+6+b-1=0\\ \Rightarrow 2a-b=5,故選\bbox[red,2pt]{(C)}$$
解答:$$x-3為f(x)=x^3+ax^2 -x+12的因式\Rightarrow f(3)=0 \Rightarrow 27+9a-3+12=0 \Rightarrow a=-4\\ \Rightarrow f(x)=x^3-4x^2 -x+12 \Rightarrow f(-2)=-8-16+2+12 =-10,故選\bbox[red,2pt]{(A)}$$
解答:$$\alpha,\beta為{x^2 \over 2}+{x\over 3}={1\over 4}之兩根 \Rightarrow \cases{\alpha +\beta= -2/3\\ \alpha\beta=-1/2} \Rightarrow {\alpha+\beta \over \alpha\beta} ={-2/3\over -1/2} = {4\over 3},故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{a= 2^{14} \\ b=4^6 =(2^2)^6 =2^{12} \\ c=8^5 = (2^3)^5 =2^{15}} \Rightarrow c \gt a\gt b,故選\bbox[red,2pt]{(C)}$$
解答:$$\cases{a=\log 3 \\ b=\log 4 },並令x=2^{a/b} \Rightarrow \log_2 x={a\over b}= {\log 3\over \log 4} ={1\over 2}\log_2 3 =\log_2 \sqrt 3 \Rightarrow x=\sqrt 3,故選\bbox[red,2pt]{(A)}$$
解答:$$x^2\gt x \Rightarrow x^2-x\gt 0 \Rightarrow x(x-1)\gt 0 \Rightarrow x\gt 1或x\lt 0,故選\bbox[red,2pt]{(D)}$$
解答:
$$所圍區域如上圖梯形ABCD,其面積=(\overline{BC}+\overline{AD})\times \overline{AB}\div 2= (6+2)\times 4\div 2=16\\,故選\bbox[red,2pt]{(B)}$$
解答:$$y=mx代入x^2+y^2=10x+10y-45 \Rightarrow x^2+m^2x^2=10x+10mx-45 \\\Rightarrow (m^2+1)x^2-10(m+1)x+45=0 有解(有交點) \Rightarrow 判別式\ge 0 \Rightarrow 100(m+1)^2-180(m^2+1)\ge 0\\ \Rightarrow 2m^2-5m+2\le 0 \Rightarrow (2m-1)(m-2)\le 0 \Rightarrow {1\over 2}\le m\le 2 \Rightarrow m的最大值為2,故選\bbox[red,2pt]{(C)}$$
解答:$$令\cases{A(-2,3)\\ B(4,-5)},則\cases{\overline{AB}= 10為直徑 \\\overline{AB}中點C(1,-1)為圓心} \Rightarrow 圓方程式:(x-1)^2 +(y+1)^2=5^2,故選\bbox[red,2pt]{(D)}$$
解答:$$7+9+11+\cdots+(2n-1)= \sum_{k=4}^n (2k-1) =2\sum_{k=4}^n k-\sum_{k=4}^n 1=(n+4)(n-3)-(n-3)=2016\\ \Rightarrow n^2-9=2016 \Rightarrow n^2=2025 \Rightarrow n=45,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{a_1=48\\ a_4=a_1r^3=-6} \Rightarrow {a_1r^3\over a_1}={-6\over 48} \Rightarrow r=-{1\over 2} \Rightarrow S(5)={a_1(1-r^5)\over 1-r} ={48(1+{1\over 32})\over 3/2} =33\\,故選\bbox[red,2pt]{(B)}$$
解答:$$3個大人挑一人排最前面,剩下2個大人挑一人排最後面,剩下1個大人及4個小孩任意排列\\,因此共有排法:C^3_1C^2_15! =3\times 2\times 120=720,故選\bbox[red,2pt]{(B)}$$
解答:$$C^7_4C^n_2=350 \Rightarrow 35\times {n(n-1)\over 2} =350 \Rightarrow n^2-n-20=0 \Rightarrow (n-5)(n+4)=0\\ \Rightarrow n=5,故選\bbox[red,2pt]{(B)}$$
解答:$${300\over 300+250+200}\times 45 = {2\over 5}\times 45=18,故選\bbox[red,2pt]{(A)}$$
解答:$$x_i=50,50,60,60,70,70 \Rightarrow \bar x=60 \Rightarrow x_i-\bar x=-10,-10,0,0,10,10\\ \Rightarrow (x_i-\bar x)^2 =100,100,0,0, 100,100 \Rightarrow \sum(x_i-\bar x)^2 = 400 \\ \Rightarrow \sqrt{400\over 6} =\sqrt{k\over 6} \Rightarrow k=400,故選\bbox[red,2pt]{(C)}$$
============================= END =============================
解答:$$令\cases{A(-2,3)\\ B(4,-5)},則\cases{\overline{AB}= 10為直徑 \\\overline{AB}中點C(1,-1)為圓心} \Rightarrow 圓方程式:(x-1)^2 +(y+1)^2=5^2,故選\bbox[red,2pt]{(D)}$$
解答:$$7+9+11+\cdots+(2n-1)= \sum_{k=4}^n (2k-1) =2\sum_{k=4}^n k-\sum_{k=4}^n 1=(n+4)(n-3)-(n-3)=2016\\ \Rightarrow n^2-9=2016 \Rightarrow n^2=2025 \Rightarrow n=45,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{a_1=48\\ a_4=a_1r^3=-6} \Rightarrow {a_1r^3\over a_1}={-6\over 48} \Rightarrow r=-{1\over 2} \Rightarrow S(5)={a_1(1-r^5)\over 1-r} ={48(1+{1\over 32})\over 3/2} =33\\,故選\bbox[red,2pt]{(B)}$$
解答:$$3個大人挑一人排最前面,剩下2個大人挑一人排最後面,剩下1個大人及4個小孩任意排列\\,因此共有排法:C^3_1C^2_15! =3\times 2\times 120=720,故選\bbox[red,2pt]{(B)}$$
解答:$$C^7_4C^n_2=350 \Rightarrow 35\times {n(n-1)\over 2} =350 \Rightarrow n^2-n-20=0 \Rightarrow (n-5)(n+4)=0\\ \Rightarrow n=5,故選\bbox[red,2pt]{(B)}$$
解答:$${300\over 300+250+200}\times 45 = {2\over 5}\times 45=18,故選\bbox[red,2pt]{(A)}$$
解答:$$x_i=50,50,60,60,70,70 \Rightarrow \bar x=60 \Rightarrow x_i-\bar x=-10,-10,0,0,10,10\\ \Rightarrow (x_i-\bar x)^2 =100,100,0,0, 100,100 \Rightarrow \sum(x_i-\bar x)^2 = 400 \\ \Rightarrow \sqrt{400\over 6} =\sqrt{k\over 6} \Rightarrow k=400,故選\bbox[red,2pt]{(C)}$$
============================= END =============================
解題僅供參考,其他身障升大學試題及詳解





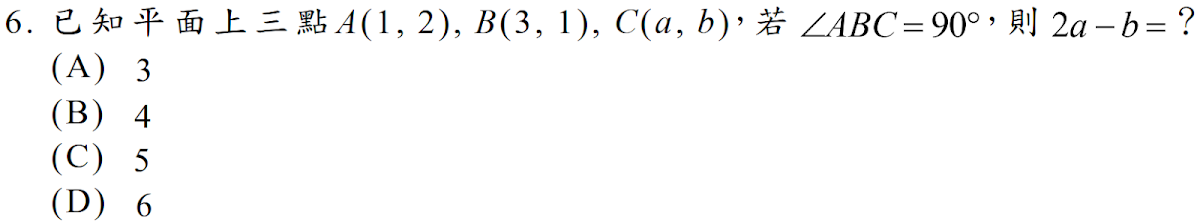















沒有留言:
張貼留言