102 學年度身心障礙學生升學大專校院甄試甄試類(群)組別:四技二專組-數學(C)
單選題,共 20 題,每題 5 分
解答:$$假設\cases{A(1,3)\\ B(3,5)\\ C(2,0)\\ D(3,a)} \Rightarrow \cases{\overrightarrow{AB}= (2,2)\\ \overrightarrow{CD} =(1,a)},依題意\overleftrightarrow{AB}\parallel \overleftrightarrow{CD} \Rightarrow {2\over 1}={2\over a} \Rightarrow a=1,故選\bbox[red,2pt]{(A)}$$
解答:$$\cases{\begin{vmatrix} a & 1\\ 2 & 3\end{vmatrix} = 3a-2\\[1ex] \begin{vmatrix} 1 & b\\ 1 & 2\end{vmatrix} = 2-b\\[1ex] \begin{vmatrix} 3 & 1\\ 2 & 1\end{vmatrix} =1} \Rightarrow \cases{3a-2=1 \\ 2-b=1} \Rightarrow \cases{a=1\\ b=1} \Rightarrow a+b=2,故選\bbox[red,2pt]{(B)}$$
解答:$$假設\cases{1斤橘子x元\\ 1斤香蕉y元} \Rightarrow \cases{3x+ 5y=350\\ 2x+y=140} \Rightarrow \cases{x=50\\ y=40} \Rightarrow x+y= 90,故選\bbox[red,2pt]{(D)}$$
解答:$$g(x)h(x)=x(x+1) = x^2+1 =x^2+x+1-1=f(x)-1 \Rightarrow 餘式為-1,故選\bbox[red,2pt]{(B)}$$
解答:$$\begin{vmatrix} 1 & 2 & 1\\ 1 & a & 2\\ 3 & 1 & 2\end{vmatrix} =2a+13 -3a-6 = -a+7=0 \Rightarrow a=7,故選\bbox[red,2pt]{(D)}$$
解答:$$x^2-5x-6\lt 0 \Rightarrow (x-6)(x+1)\lt 0 \Rightarrow -1\lt x\lt 6 \Rightarrow 奇數解x= 1, 3, 5,共三個,故選\bbox[red,2pt]{(A)}$$
解答:$$\cases{骰子出現偶數的機率=1/2\\ 硬幣出現正面的機率=1/2} \Rightarrow 偶數且正面的機率={1\over 2}\times {1\over 2}={1\over 4},故選\bbox[red,2pt]{(C)}$$
解答:$$\cases{抽中1000元的機率=2/10\\ 抽中600元的機率=3/10\\ 抽中200元的機率=5/10} \Rightarrow 期望值=1000\times {2\over 10}+ 600\times {3\over 10}+ 200\times {5\over 10} = 480\\,故選\bbox[red,2pt]{(C)}$$
解答:$$\cases{a_1+ a_2+a_3=15\\ a_4+a_5= 20} \Rightarrow \cases{a_1+ a_1+d+a_1+2d= 15\\ a_1+3d+ a_1+4d= 20} \Rightarrow \cases{3a_1+ 3d=15\\ 2a_1+7d =20} \Rightarrow \cases{a_1= 3\\ d=2} \\ \Rightarrow a_{10}= a_1+9d = 3+18=21,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{P(0,0)\\ Q(1,1)\\ R(2,3)} \Rightarrow \cases{\overrightarrow{PQ} =(1,1) \\\overrightarrow{PR} =(2,3)} \Rightarrow \vec u=5\overrightarrow{PQ}-2\overrightarrow{PR} =(5,5)-(4,6)=(1,-1)\\ 又\vec u\bot \vec v \Rightarrow \vec u\cdot \vec v=0 \Rightarrow (1,-1)\cdot (2,a)=0 \Rightarrow 2-a=0 \Rightarrow a=2,故選\bbox[red,2pt]{(C)}$$
解答:$$\sqrt{(1-4)^2+(1-k)^2} =k \Rightarrow 9+(k-1)^2 =k^2 \Rightarrow 2k=10\Rightarrow k=5,故選\bbox[red,2pt]{(B)}$$
解答:$$\tan \theta=1 \Rightarrow \theta=45^\circ \Rightarrow a=\sin 45^\circ ={1\over \sqrt 2} \Rightarrow 2a^2+1 =1+1=2,故選\bbox[red,2pt]{(C)}$$
解答:$$4\sin^2\theta -4\sin \theta+1=0 \Rightarrow (2\sin \theta-1)^2=0 \Rightarrow \sin\theta ={1\over 2}\\ \Rightarrow \cos^2\theta =1-{1\over 4}={3\over 4} \Rightarrow 4\cos^2\theta =3,故選\bbox[red,2pt]{(C)}$$
解答:$$f(x)=ax^2(x+5) +5x(x+5)+ 2(x+5) \Rightarrow f(-2)=0 \Rightarrow 12a-30+6 \Rightarrow a=2,故選\bbox[red,2pt]{(D)}$$
解答:$$令\cases{f(x)= ax^2+bx-2 \\ g(x)=bx^2-4x+a},依題意\cases{f(1)=0\\ g(2)=0} \Rightarrow \cases{a+b-2=0\\ 4b-8+a=0} \Rightarrow \cases{a=0\\ b=2}\\ \Rightarrow a-b=-2,故選\bbox[red,2pt]{(A)}$$
解答:$$\log_2 25\times \log_3 7\times \log_5 9\times \log_7 8= {2\log 5\over \log 2} \times {\log 7\over \log 3} \times {2\log 3\over \log 5} \times {3\log 2\over \log 7} =12,故選\bbox[red,2pt]{(B)}$$
解答:$$26^2\times 10^4= 6760000 ,故選\bbox[red,2pt]{(D)}$$
解答:$$將x=2代入圓方程式:(x+1)^2 +(y-1)^2=5^2 \Rightarrow 9+(y-1)^2 = 25 \Rightarrow y-1=\pm 4 \\\Rightarrow \cases{y=5\\ y=-3} \Rightarrow 交點為\cases{(2,5)\\ (2,-3)} \Rightarrow a+b=5-3=2,故選\bbox[red,2pt]{(A)}$$
解答:$$\log_a b,4,8成等比\Rightarrow 4^2=8\log_a b \Rightarrow \log_a b=2 \Rightarrow a^2=b代入b-a=2 \Rightarrow a^2-a=2\\ \Rightarrow (a-2)(a+1)=0 \Rightarrow a=2\Rightarrow b=a^2=4 \Rightarrow a+b=2+4=6,故選\bbox[red,2pt]{(B)}$$
========================= END ==============================
解題僅供參考,其他歷屆試題及詳解




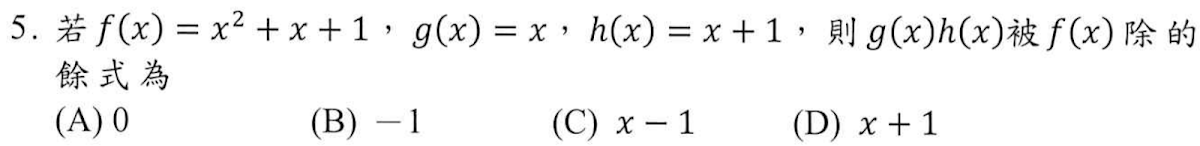





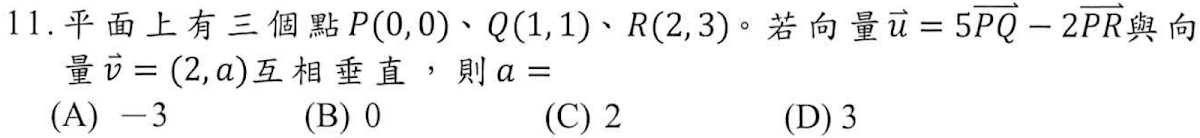









沒有留言:
張貼留言