103 學年度身心障礙學生升學大專校院甄試甄試類(群)組別:四技二專組-數學(C)
單選題,共 20 題,每題 5 分
解答:$$\overline{PA}: \overline{QA}=3:1 \Rightarrow A=(P+3Q)/4 = ({-5+21\over 4}, {5+3\over 4}) =(4,2),故選\bbox[red,2pt]{(D)}$$解答:$$\sin \theta-\cos\theta={1\over 3} \Rightarrow (\sin \theta-\cos\theta)^2 = 1-2\sin\theta \cos \theta={1\over 9} \Rightarrow 2\sin\theta \cos\theta ={8\over 9} \\ \Rightarrow (\sin \theta+\cos\theta)^2 =1+2\sin\theta \cos\theta =1+{8\over 9}= {17\over 9},故選\bbox[red,2pt]{(C)}$$
解答:$$正\triangle 邊長=\overline{OA}= 2 \Rightarrow B(2\cos 60^\circ, 2\sin 60^\circ)=(1,\sqrt 3),故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{A(1,1)\\ B(5,2)\\ C(7,0)} \Rightarrow \cases{\overrightarrow{AB} =(4,1)\\ \overrightarrow{AC} =(6,-1)} \Rightarrow \overrightarrow{AB} \cdot \overrightarrow{AC} =24-1=23,故選\bbox[red,2pt]{(A)}$$
解答:$$求x項係數,原多項式只需考慮(1+x)(1+x)(1+x)= 1+3x+3x^2+x^3 \Rightarrow x項係數=3\\,故選\bbox[red,2pt]{(C)}$$
解答:$$f(x)=2x^3-x^2-x-3 = x^2(2x-1)-(x+3) \Rightarrow \cases{f(-3/2)={9\over 4}\cdot (-4)-{3\over 2}\ne 0\\ f(-1/2)={1\over 4} \cdot (-2)-{5\over 2}\ne 0\\ f(1/2)= 0-{7\over 2} \ne 0\\ f(3/2) = {9\over 4}\cdot 2-{9\over 2}=0} \\ \Rightarrow x={3\over 2}為方程式的解,故選\bbox[red,2pt]{(D)}$$
解答:$$ \begin{vmatrix}3 & 2 & 6\\101 & 68 & 204\\257 & 170 & 512\end{vmatrix} \xrightarrow{-34r_1+r_2,-85r_1+r_3} \begin{vmatrix}3 & 2 & 6\\-1 & 0 & 0\\2 & 0 & 2\end{vmatrix} =4,故選\bbox[red,2pt]{(A)}$$
解答:$${-1+5i\over 1+i} ={(-1+5i)(1-i)\over (1+i)(1-i)} ={4+6i \over 2} =2+3i,故選\bbox[red,2pt]{(B)}$$
解答:$$\sum_{k=0}^9 (2^k+2k) =\sum_{k=0}^9 2^k+2\sum_{k=0}^9k ={1-2^{10}\over 1-2} +2\cdot 45= 1023+90 = 1113,故選\bbox[red,2pt]{(C)}$$
解答:$$\left( {9\over 4} \right)^{-3/2}\left( {1\over 8} \right)^{2/3} =\left( {3\over 2} \right)^{-3 }\left( {1\over 2} \right)^{2 } ={8\over 27} \cdot {1\over 4} ={2\over 27},故選\bbox[red,2pt]{(C)}$$
解答:$$\log_x 216={3\over 2} \Rightarrow x^{3/2} =216=6^3 \Rightarrow \sqrt x=6 \Rightarrow x=36,故選\bbox[red,2pt]{(D)}$$
解答:$$n!=132\cdot (n-2)! \Rightarrow 132={n!\over (n-2)!} =n(n-1) \Rightarrow n^2-n-132=0 \Rightarrow (n-12)(n+11)=0\\ \Rightarrow n=12,故選\bbox[red,2pt]{(B)}$$
解答:$$1-兩人都沒投進的機率=1-{2\over 3}\cdot {1\over 3}={7\over 9},故選\bbox[red,2pt]{(C)}$$
解答:$$3x^2+7y^2+18x-28y=0 \Rightarrow 3(x^2+6x+9)+7(y^2 -4y+4)=27+28 \\ \Rightarrow 3(x+3)^2+ 7(y-2)^2=55 \Rightarrow 圓心(-3,2),故選\bbox[red,2pt]{(A)}$$
解答:$$\lim_{x\to 9}{\sqrt x-3\over x^2-81} =\lim_{x\to 9}{\sqrt x-3\over (x+9)(\sqrt x+3)(\sqrt x-3)} =\lim_{x\to 9}{1 \over (x+9)(\sqrt x+3) } = {1\over 18\cdot 6} ={1\over 108}\\,故選\bbox[red,2pt]{(D)}$$
解答:$$(A) \log_{1/2}6 ={\log_2 6\over \log_2 1/2} =-\log_2 6 \lt 0\\ (B)\log_{1/3} 2= {\log_3 2\over \log_3 {1/3}} =-\log_3 2\lt 0\\ (C)0\lt \log_3 2\lt 1\\ (D)\log_2 3\gt 1\\ \Rightarrow \log_2 3最大,故選\bbox[red,2pt]{(D)}$$
解答:
$$f(x)=12-3x^2=0 \Rightarrow x=\pm 2 \Rightarrow 所圍面積=\int_{-2}^2 12-3x^2\,dx = \left. \left[ 12x-x^3\right] \right|_{-2}^2 \\ =16-(-16)=32,故選\bbox[red,2pt]{(C)}$$
解答:$$過(2,-3)且斜率為m之直線L:y=m(x-2)-3代入圓C \\\Rightarrow x^2+(mx-2m-3)^2-6x+4(mx-2m-3)+11=0 \Rightarrow 判別式=0 \Rightarrow m=-1\\ 另解:x^2+y^2-6x+4y+11=0 \Rightarrow 2x+2yy'-6+4y'=0\\,將(2,-3)代入可得: 4-6y'-6+4y'=0 \Rightarrow y'=-1 (斜率)\\ 因此,L:y=-(x-2)-3 \Rightarrow x+y+1=0,故選\bbox[red,2pt]{(A)}$$
解答:
解答:
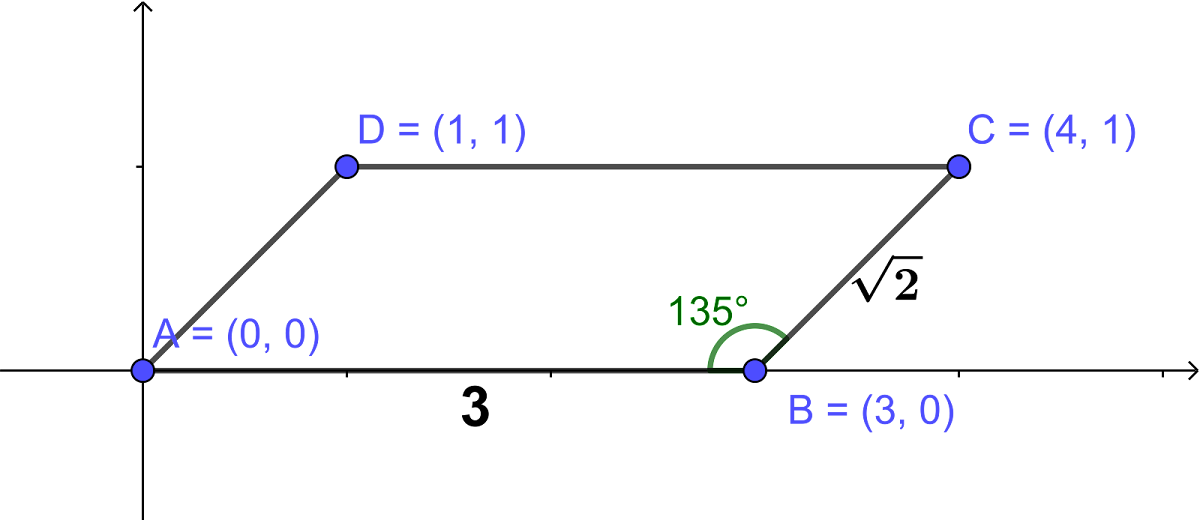
$$令\cases{A(0,0)\\ B(3,0)},則\cases{C(4,1)\\ D(1,1)} \Rightarrow \overline{BD} =\sqrt{2^2+1^2} =\sqrt 5,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{x\ge 7 \Rightarrow 2x-5\le x-7 \Rightarrow x\le -2\Rightarrow 無解\\ 5/2\le x\le 7 \Rightarrow 2x-5\le 7-x \Rightarrow x\le 4 \Rightarrow 5/2\le x\le 4\\ x\le 5/2 \Rightarrow 5-2x\le 7-x \Rightarrow -2\le x \Rightarrow -2\le x\le 5/2} \Rightarrow -2\le x\le 4 \\\Rightarrow x=-2,-1,0,1,2,3,4,共7個整數,故選\bbox[red,2pt]{(B)}$$
========================== END ==================================
解題僅供參考,其他歷屆試題及詳解







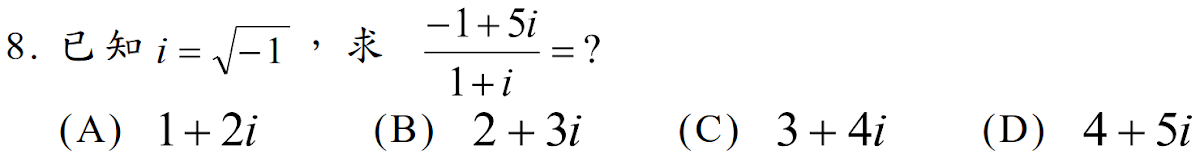













沒有留言:
張貼留言