國立竹東高級中學 112 學年度第一次教師甄選
一、填充題:每題5 分,共50 分
解答:$$將2023個數字切成前段與後段,對每個數字而言,可以有兩種選擇(前段或後段)\\ 因此共有2^{2023}種拆法,其中需扣除不合條件的拆法;也就是將數字由小排到大,然後直接切兩塊,\\有2023種切法,這種切法就沒有a_i存在,因此共有\bbox[red, 2pt]{2^{2023}-2023}種$$解答:$$\begin{bmatrix}0 & 1 & -3 & 2 \\1 & 0 & 2 & -1 \end{bmatrix} \xrightarrow{3r_1+r_2\to r_2} \begin{bmatrix}0 & 1 & -3 & 2 \\1 & 3 & -7 & 5 \end{bmatrix} \xrightarrow {-17r_1} \begin{bmatrix}0 & -17 & 51 & -34 \\1 & 3 & -7 & 5 \end{bmatrix} \\ \xrightarrow{5r_2+ r_1 \to r_1} \begin{bmatrix}5 & -2 & 16 & -9 \\1 & 3 & -7 & 5 \end{bmatrix} \Rightarrow \begin{bmatrix}a & b \\c & d \end{bmatrix}=\bbox[red, 2pt]{\begin{bmatrix}5 & -2 \\1 & 3 \end{bmatrix}}$$
解答:$$本題\bbox[red, 2pt]{送分}$$
解答:$$f(x)=0有一根為2 \Rightarrow f(x)=a(x-2)(x-b)\\ \Rightarrow g(x)=f(f(x))= a[a(x-2)(x-b)-2][a(x-2)(x-b)-b] \\=a^3 \left(x^2-(b+2)x+2b-{2\over a}\right) \left( x^2-(b+2)x+2b-{b\over a}\right) \equiv a^3f_1(x)f_2(x)\\ \Rightarrow \cases{\cases{f_1=(x-5)^2\\ f_2的判別式\lt 0} \Rightarrow \cases{a=-2/9\\ b=8}\\ \cases{f_2=(x-5)^2\\ f_1的判別式\lt 0} \Rightarrow \cases{a=-8/9\\ b=8}但f_1判別式\not \lt 0}\\ \Rightarrow f(0)=2ab=2\cdot (-{2\over 9})\cdot 8 =\bbox[red, 2pt]{-{32\over 9}}$$
解答:$$令\cases{\alpha=\sqrt 3+\sqrt 2\\ \beta=\sqrt 3-\sqrt 2} \Rightarrow \cases{\alpha+\beta=2\sqrt 3\\ \alpha\beta =1 \Rightarrow \beta=1/\alpha} \\ 現在a_n=\alpha^{2n} \Rightarrow b_n=\alpha^{2n}+{1\over \alpha^{2n}} = \alpha^{2n}+\beta^{2n} \\ \Rightarrow b_{2023}=(\sqrt 3+\sqrt 2)^{4046}+(\sqrt 3-\sqrt 2)^{4046} =(5+2\sqrt 6)^{2023}+(5-2\sqrt 6)^{2023}\\ =\sum_{n=0}^{2023}{2023\choose n}5^n(2\sqrt 6)^{2023-n} +\sum_{n=0}^{2023}{2023\choose n}5^n(-2\sqrt 6)^{2023-n} = 2\sum_{k=1}^{1012}{2023\choose 2k-1}5^{2k-1}(2\sqrt 6)^{2024-2k}\\ 以上每一項均為10的倍數,因此b_{2023}的個位數字為\bbox[red, 2pt]0$$
解答:$$假設\cases{O=(0,0)\\ A(z_1)\\ B(z_2)},由\cases{|z_1|=1\\ |z_2|=\sqrt 2\\ |z_1-z_2|=1} \Rightarrow \cases{\overline{OA}=1\\ \overline{OB}=\sqrt 2\\ \overline{AB}=1} \Rightarrow \cases{\angle OAB=90^\circ \\\angle AOB=\angle OBA=45^\circ}\\ 因此假設\cases{A(\cos \theta,\sin \theta)\\ B(\sqrt 2\cos(\theta+{\pi\over 4}), \sqrt 2\sin (\theta+{\pi\over 4}))\\ P(1,0)}\\ \Rightarrow 欲求之|z_1-1|^2 +|z_2-1|^2=\overline{AP}^2+\overline{BP}^2\equiv f(\theta)\\ \Rightarrow f(\theta) =(\cos \theta-1)^2+\sin^2\theta +(\sqrt 2\cos(\theta+{\pi\over 4})-1)^2 +2\sin^2(\theta+{\pi\over 4})\\ =5-2\cos\theta-2\sqrt 2\cos(\theta+{\pi\over 4})\\ 因此f'(\theta)=0 \Rightarrow 2\sin\theta+2\sqrt 2\sin(\theta+{\pi\over 4})=0 \Rightarrow 2\sin \theta+\cos\theta=0\\ \Rightarrow \tan \theta=-{1\over 2} \Rightarrow \cases{\sin \theta=-1/\sqrt 5\\ \cos\theta=2/\sqrt 5} \\\Rightarrow f(\tan^{-1}(-{1\over 2})) =5-2\cdot {2\over \sqrt 5}-2({2\over \sqrt 5}+{1\over \sqrt 5})=5-{10\over \sqrt 5}= \bbox[red, 2pt]{5-2\sqrt 5}$$
解答:
$$假設P=\overline{BE}\cap \overline{AD}且\overline{DQ} \parallel \overline{BE},如上圖\\ 由於\cases{\overline{BE}是\angle B的角平分線\\ \overline{AD}\bot \overline{BE}} \Rightarrow \overline{BE}是\overline{AD}的中垂線\Rightarrow \overline{AP}=\overline{PD}=\overline{AD}\div 2=2\\ 又\cases{\overline{BD}=\overline{DC}\\ \overline{DQ} \parallel \overline{BE}} \Rightarrow \overline{DQ}={1\over 2}\overline{BE}=2;同理,\overline{PE}={1\over 2}\overline{DQ}=1 \Rightarrow \overline{BP}=4-1=3\\ 因此\cases{\overline{CD}=\overline{DB} =\overline{AB}= \sqrt{3^2+2^2}= \sqrt{13} \\ \overline{CQ}=\overline{QE}= \overline{AE}=\sqrt{2^1+1^2}= \sqrt 5} \Rightarrow \triangle ABC周長=\bbox[red, 2pt]{3(\sqrt {13}+\sqrt 5)}$$
解答:$$圖形為凹向上,且y截距\ge 0,即\cases{3-p\ge 0\\ p+4\ge 0} \Rightarrow 3\ge p\ge -4 \Rightarrow p=-4,-3,\dots, 3,共\bbox[red,2pt]8個\\註:p=3時,y=f(x)為一直線,仍符合要求$$
解答:$$\cases{f(\alpha) =\beta\\ f(-2-\alpha)=-4-\beta} \Rightarrow 對稱中心({\alpha+(-2-\alpha)\over 2},{\beta+(-4-\beta)\over 2})=(-1,-2) \\ \Rightarrow f''(-1)=0 \Rightarrow 6a(-1)+2b=0 \Rightarrow b=3a\\ ad=3 \Rightarrow \cases{(a,d)=(3,1) \Rightarrow b=9\\ (a,d)=(-3,-1) \Rightarrow b=-9\\ (a,d)=(1,3) \Rightarrow b=3\\ (a,d)=(-1,-3) \Rightarrow b=-3} \Rightarrow \cases{f_1=3x^3+9x^2+cx+1 \\f_2=-3x^3-9x^2+cx-1 \\f_3=x^3+3x^2+cx+3 \\f_4=-x^3-3x^2+cx-3 }\\ 再由f(-1)=-2 \Rightarrow \cases{f_1=3x^3+9x^2+9x+1 \\f_2=-3x^3-9x^2-5x-1 \\f_3=x^3+3x^2+7x+3 \\f_4=-x^3-3x^2-3x-3} \Rightarrow \cases{f_1'=9x^2+18+9\\ f_2'=-9x^2-18x-5 \\f_3'=3x^2+6x+7\\ f_4'=-3x^2-6x-3}\\ \Rightarrow \cases{f_1'的判別式=0 \\ f_2'的判別式>0 \\ f_3'的判別式\lt 0 \\ f_4'的判別式=0 } \Rightarrow 只有f_2符合條件(2),因此f(x)=f_2=\bbox[red, 2pt]{-3x^3-9x^2-5x-1}$$
解答:$$假設總題數為m,m 必須是4的倍數也是6的倍數,也就是12的倍數\\又\cases{乙做錯9題\\ 同時做錯m/6题} \Rightarrow {m\over 6}\le 9 \Rightarrow m\le 54 \cdots(1)\\ \cases{甲做對3m/4\\ 乙做對m-9題\\ 同時做對n(\ge 20)題} \Rightarrow \cases{3m/4\ge 20\\ m-9\ge 20} \Rightarrow m\ge 29 \cdots(2)\\ 由(1)及(2)且m是12的倍數 \Rightarrow m=48或36\\ \\ \Rightarrow \begin{array}{l|cc} &m=48 &m=36\\\hline 甲對乙也對的題數(n) & 35 & 24\\ 甲錯乙也錯的題數&8&6 \\ 甲對乙錯的題數&1& 3\\ 甲錯乙對的題數& 4& 3\\\hline\end{array}\Rightarrow 所有的n之和=35+24=\bbox[red, 2pt]{59}$$
解答:$$y=\sqrt{4+4\sin t}+\sqrt{2+2\cos t} \Rightarrow y'=0 \Rightarrow {\cos t\over \sqrt{1+\sin t}}-{\sin t\over \sqrt{2+2\cos t}}=0\\ \Rightarrow 2\cos^2 t+2\cos^3t=\sin^2t+\sin^3t,此時取\cases{\sin t=a/c\\ \cos t=b/c},a^2+b^2=c^2\\ \Rightarrow 2\cdot {b^2\over c^2}+2\cdot {b^3\over c^3}={a^2\over c^2}+{a^3\over c^3} \Rightarrow c(a^2-2b)=2b^3-a^3 \Rightarrow \sqrt{a^2+b^2}(a^2-2b)=2b^3-a^3 \\ \Rightarrow 3a=4b \Rightarrow \tan t ={4\over 3} \Rightarrow \cases{\sin t=4/5\\ \cos t=3/5} \Rightarrow y=\sqrt{4+{16\over 5}}+ \sqrt{2+{6\over 5}} \\={10\over \sqrt 5}=\bbox[red,2pt]{2\sqrt 5}$$
解答:$$x=a 代入圓C及拋物線\Gamma 可得\cases{\overline{PA}=a^2/5\\ \overline{PB}=2-\sqrt{4-a^2}} \Rightarrow \lim_{a\to 0}{\overline{PA} \over \overline{PB}} =\lim_{a\to 0} {a^2/5\over 2-\sqrt{4-a^2}} \\ =\lim_{a\to 0} {{d\over da}a^2/5\over {d\over da}(2-\sqrt{4-a^2})} =\lim_{a\to 0} {2a/5\over a/\sqrt{4-a^2}}=\lim_{a\to 0} {2\over 5}\sqrt{4-a^2} =\bbox[red, 2pt]{4\over 5}$$
解答:$${a^2+ab+b^2\over ab-1}=k\\ \text{Cases I}\; ab=0 \Rightarrow \cases{a=b=0 \Rightarrow k=\color{blue}0\\ a=0,b\ne 0 \Rightarrow k=-b^2 \lt 0,不合\\ a\ne 0,b=0 \Rightarrow k=-a^2 \lt 0 ,不合}\\ \text{Cases II}\; a=b\ne 0 \Rightarrow k={3a^2\over a^2-1} =3+{3\over a^2-1} = \color{blue}4 (a=b=2)\\ \text{Cases III }a\gt b=1 \Rightarrow k={a^2+a+1\over a-1}=(a+2)+{3\over a-1} =\color{blue}7(a=2)\\ 現在我們已有k=\bbox[red, 2pt]{0,4,7}, 接著我們要證明整數 k\not \gt 7...$$
解答:$$\tan{C\over 2}\tan{A-B\over 2}=\tan(90^\circ-{A+B\over 2}) \tan{A-B\over 2}= \cot{A+B\over 2} \tan{A-B\over 2} \\ ={\cos( (A+B)/2) \over \sin((A+B)/2)}\cdot {\sin((A-B)/2)\over \cos((A-B)/2)} ={\sin A-\sin B\over \sin A+\sin B}(積化和差公式)\\ =\bbox[red, 2pt]{a-b\over a+b}(用正弦定理{a\over \sin A}={b\over \sin B})$$
解答:$$\lim_{n\to \infty}\left( {1\over n}\sqrt{4-({1\over n})^2} + {1\over n}\sqrt{4-({2\over n})^2} + \cdots + {1\over n}\sqrt{4-({n\over n})^2} \right) =\lim_{n\to \infty} \sum_{k=1}^n {1\over n}\sqrt{4-({k\over n})^2} \\=\int_0^1 \sqrt{4-x^2}\,dx =\int_0^{\pi/6} 4\cos^2\theta \,d\theta \quad(取x=2\sin \theta) =\int_0^{\pi/6} 2\cos 2\theta+2\,d\theta =\bbox[red,2pt]{{\sqrt 3\over 2}+{\pi\over 3}}$$
解答:$$P在直線x+1={y\over 2}={3-z\over -2}上\Rightarrow P(t-1,2t,2t+3),t\in \mathbb R\\ \Rightarrow \overline{AP}+\overline{BP}=\sqrt{(t-9)^2+4t^2+(2t-9)^2}+\sqrt{(t-8)^2+(2t-13)^2 +(2t-10)^2} \\=3\left(\sqrt{(t-3)^2+3^2}+\sqrt{(t-6)^2+1^2}\right) = 3(\overline{RS}+ \overline{RT}),其中\cases{R(t,0)\in x軸\\ S(3,3)\\ T(6,1)}\\ \Rightarrow 最小值=3\overline{ST'},T'=(6,-1) \Rightarrow \overline{AP} +\overline{BP}的最小值=3\sqrt{(6-3)^2 +(-1-3)^2}= \bbox[red,2pt]{15}\\ 此時R=\overline{ST'}與x軸的交點,\overleftrightarrow{ST'}:y=-{4\over 3}x+7與x軸交於({21\over 4},0)\\ 也就是t={21\over 4} \Rightarrow P=\bbox[red,2pt]{\left({17\over 4}, {21\over 2},{27\over 2} \right)}$$
解答:$$\cases{f(\alpha) =\beta\\ f(-2-\alpha)=-4-\beta} \Rightarrow 對稱中心({\alpha+(-2-\alpha)\over 2},{\beta+(-4-\beta)\over 2})=(-1,-2) \\ \Rightarrow f''(-1)=0 \Rightarrow 6a(-1)+2b=0 \Rightarrow b=3a\\ ad=3 \Rightarrow \cases{(a,d)=(3,1) \Rightarrow b=9\\ (a,d)=(-3,-1) \Rightarrow b=-9\\ (a,d)=(1,3) \Rightarrow b=3\\ (a,d)=(-1,-3) \Rightarrow b=-3} \Rightarrow \cases{f_1=3x^3+9x^2+cx+1 \\f_2=-3x^3-9x^2+cx-1 \\f_3=x^3+3x^2+cx+3 \\f_4=-x^3-3x^2+cx-3 }\\ 再由f(-1)=-2 \Rightarrow \cases{f_1=3x^3+9x^2+9x+1 \\f_2=-3x^3-9x^2-5x-1 \\f_3=x^3+3x^2+7x+3 \\f_4=-x^3-3x^2-3x-3} \Rightarrow \cases{f_1'=9x^2+18+9\\ f_2'=-9x^2-18x-5 \\f_3'=3x^2+6x+7\\ f_4'=-3x^2-6x-3}\\ \Rightarrow \cases{f_1'的判別式=0 \\ f_2'的判別式>0 \\ f_3'的判別式\lt 0 \\ f_4'的判別式=0 } \Rightarrow 只有f_2符合條件(2),因此f(x)=f_2=\bbox[red, 2pt]{-3x^3-9x^2-5x-1}$$
解答:$$假設總題數為m,m 必須是4的倍數也是6的倍數,也就是12的倍數\\又\cases{乙做錯9題\\ 同時做錯m/6题} \Rightarrow {m\over 6}\le 9 \Rightarrow m\le 54 \cdots(1)\\ \cases{甲做對3m/4\\ 乙做對m-9題\\ 同時做對n(\ge 20)題} \Rightarrow \cases{3m/4\ge 20\\ m-9\ge 20} \Rightarrow m\ge 29 \cdots(2)\\ 由(1)及(2)且m是12的倍數 \Rightarrow m=48或36\\ \\ \Rightarrow \begin{array}{l|cc} &m=48 &m=36\\\hline 甲對乙也對的題數(n) & 35 & 24\\ 甲錯乙也錯的題數&8&6 \\ 甲對乙錯的題數&1& 3\\ 甲錯乙對的題數& 4& 3\\\hline\end{array}\Rightarrow 所有的n之和=35+24=\bbox[red, 2pt]{59}$$
解答:$$y=\sqrt{4+4\sin t}+\sqrt{2+2\cos t} \Rightarrow y'=0 \Rightarrow {\cos t\over \sqrt{1+\sin t}}-{\sin t\over \sqrt{2+2\cos t}}=0\\ \Rightarrow 2\cos^2 t+2\cos^3t=\sin^2t+\sin^3t,此時取\cases{\sin t=a/c\\ \cos t=b/c},a^2+b^2=c^2\\ \Rightarrow 2\cdot {b^2\over c^2}+2\cdot {b^3\over c^3}={a^2\over c^2}+{a^3\over c^3} \Rightarrow c(a^2-2b)=2b^3-a^3 \Rightarrow \sqrt{a^2+b^2}(a^2-2b)=2b^3-a^3 \\ \Rightarrow 3a=4b \Rightarrow \tan t ={4\over 3} \Rightarrow \cases{\sin t=4/5\\ \cos t=3/5} \Rightarrow y=\sqrt{4+{16\over 5}}+ \sqrt{2+{6\over 5}} \\={10\over \sqrt 5}=\bbox[red,2pt]{2\sqrt 5}$$
解答:$$x=a 代入圓C及拋物線\Gamma 可得\cases{\overline{PA}=a^2/5\\ \overline{PB}=2-\sqrt{4-a^2}} \Rightarrow \lim_{a\to 0}{\overline{PA} \over \overline{PB}} =\lim_{a\to 0} {a^2/5\over 2-\sqrt{4-a^2}} \\ =\lim_{a\to 0} {{d\over da}a^2/5\over {d\over da}(2-\sqrt{4-a^2})} =\lim_{a\to 0} {2a/5\over a/\sqrt{4-a^2}}=\lim_{a\to 0} {2\over 5}\sqrt{4-a^2} =\bbox[red, 2pt]{4\over 5}$$
解答:$${a^2+ab+b^2\over ab-1}=k\\ \text{Cases I}\; ab=0 \Rightarrow \cases{a=b=0 \Rightarrow k=\color{blue}0\\ a=0,b\ne 0 \Rightarrow k=-b^2 \lt 0,不合\\ a\ne 0,b=0 \Rightarrow k=-a^2 \lt 0 ,不合}\\ \text{Cases II}\; a=b\ne 0 \Rightarrow k={3a^2\over a^2-1} =3+{3\over a^2-1} = \color{blue}4 (a=b=2)\\ \text{Cases III }a\gt b=1 \Rightarrow k={a^2+a+1\over a-1}=(a+2)+{3\over a-1} =\color{blue}7(a=2)\\ 現在我們已有k=\bbox[red, 2pt]{0,4,7}, 接著我們要證明整數 k\not \gt 7...$$
解答:$$\tan{C\over 2}\tan{A-B\over 2}=\tan(90^\circ-{A+B\over 2}) \tan{A-B\over 2}= \cot{A+B\over 2} \tan{A-B\over 2} \\ ={\cos( (A+B)/2) \over \sin((A+B)/2)}\cdot {\sin((A-B)/2)\over \cos((A-B)/2)} ={\sin A-\sin B\over \sin A+\sin B}(積化和差公式)\\ =\bbox[red, 2pt]{a-b\over a+b}(用正弦定理{a\over \sin A}={b\over \sin B})$$
解答:$$\lim_{n\to \infty}\left( {1\over n}\sqrt{4-({1\over n})^2} + {1\over n}\sqrt{4-({2\over n})^2} + \cdots + {1\over n}\sqrt{4-({n\over n})^2} \right) =\lim_{n\to \infty} \sum_{k=1}^n {1\over n}\sqrt{4-({k\over n})^2} \\=\int_0^1 \sqrt{4-x^2}\,dx =\int_0^{\pi/6} 4\cos^2\theta \,d\theta \quad(取x=2\sin \theta) =\int_0^{\pi/6} 2\cos 2\theta+2\,d\theta =\bbox[red,2pt]{{\sqrt 3\over 2}+{\pi\over 3}}$$
解答:$$P在直線x+1={y\over 2}={3-z\over -2}上\Rightarrow P(t-1,2t,2t+3),t\in \mathbb R\\ \Rightarrow \overline{AP}+\overline{BP}=\sqrt{(t-9)^2+4t^2+(2t-9)^2}+\sqrt{(t-8)^2+(2t-13)^2 +(2t-10)^2} \\=3\left(\sqrt{(t-3)^2+3^2}+\sqrt{(t-6)^2+1^2}\right) = 3(\overline{RS}+ \overline{RT}),其中\cases{R(t,0)\in x軸\\ S(3,3)\\ T(6,1)}\\ \Rightarrow 最小值=3\overline{ST'},T'=(6,-1) \Rightarrow \overline{AP} +\overline{BP}的最小值=3\sqrt{(6-3)^2 +(-1-3)^2}= \bbox[red,2pt]{15}\\ 此時R=\overline{ST'}與x軸的交點,\overleftrightarrow{ST'}:y=-{4\over 3}x+7與x軸交於({21\over 4},0)\\ 也就是t={21\over 4} \Rightarrow P=\bbox[red,2pt]{\left({17\over 4}, {21\over 2},{27\over 2} \right)}$$
解題僅供參考,其他教甄試題及詳解















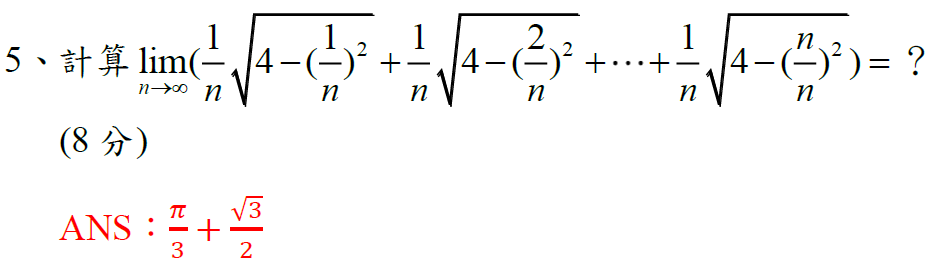

沒有留言:
張貼留言