國立基隆女中 113 學年第 2 次教師甄試 筆試試題 數學科
一、 填充題(每題 4 分,共 52 分,題號標示清楚且照順序填答,無須寫出計算過程)
解答:$$假設等差數列\langle a_n\rangle ,首項a,公差d \Rightarrow a_1+\cdots+a_{113}= {(2a+112d)\cdot 113\over 2} =2024 \\ \Rightarrow 2a+112d={4048\over 113} \Rightarrow a_m+a_n={4048\over 113},\text{ if }m+n=114\\ 兩式\cases{a_1b_1+a_2b_2+ \cdots +a_{113}b_{113}=4000\\ a_1b_{113}+ a_2b_{112}+ \cdots+a_{113}b_1=k}\\ 頭尾相加 \Rightarrow b_1(a_1+a_{113}) + b_2(a_2+a_{112})+ \cdots +b_{113}(a_{113}+a_1) =4000+k \\ \Rightarrow {4048\over 113} (b_1+b_2+ \cdots+ b_{113})=4000+k \Rightarrow {4048\over 113} \cdot 113=4000+k \Rightarrow k=\bbox[red, 2pt]{48}$$解答:$$\sum_{k=2}^{900}{2\over \sqrt {k+1}+\sqrt{k}} \lt \sum_{k=2}^{900}{1\over \sqrt k} \lt \sum_{k=2}^{900}{2\over \sqrt k+\sqrt{k-1}} \\ \Rightarrow \sum_{k=2}^{900}2(\sqrt {k+1}-\sqrt{k}) \lt \sum_{k=2}^{900}{1\over \sqrt k} \lt \sum_{k=2}^{900}2(\sqrt k -\sqrt{k-1})\\ \Rightarrow 2(\sqrt{901}-\sqrt 2) \lt \sum_{k=2}^{900}{1\over \sqrt k} \lt 2(\sqrt{900}-1)\\ \Rightarrow 2(\sqrt{901}-\sqrt 2) +1\lt \sum_{k=1}^{900}{1\over \sqrt k} \lt 2(\sqrt{900}-1)+1 \\ \Rightarrow 2(30-\sqrt 2)+1\lt \sum_{k=1}^{900}{1\over \sqrt k}\lt 59 \\左式=61-2\sqrt 2=61-2\cdot 1.414 = 58.17 \Rightarrow \sum_{k=1}^{900}{1\over \sqrt k}整數部分=\bbox[red, 2pt]{58}$$
解答:
$$面積和={\sqrt 3\over 4}x^2+{3\sqrt 3\over 2}(y^2+z^2)要最小\Rightarrow y=z\\又兩正六邊形不能重疊,因此兩正六邊形夾角最多為120^\circ,如上圖 \\ 因此x=\sqrt 3y \Rightarrow x:y:z=\bbox[red, 2pt]{\sqrt 3:1:1}$$
解答:$$此題相當於求x+y+z=20,且符合1\le x,y,z\le 12的整數解個數\\ \begin{array}{c|c|}x & y,z & 個數\\\hline 12 & y+z=8 & H^2_6\\ 11 & y+z=7& H^2_7\\ \cdots & \cdots &\cdots\\ 7& y+z=13& H^2_{11}\\\hdashline 6& y+z=14&(12,2),(11,3),\dots,(2,12),11種\\ 5&y+z=15& (12,3),\dots,(3,12),10種\\ \cdots & \cdots &\cdots \\ 1& y+z=19& (12,7),\dots, (7,12),6種\end{array} \\ 因此共有 \sum_{k=6}^{11} (H^2_k +k) =\sum_{k=6}^{11} (2k+1) =102+6= \bbox[red, 2pt]{108}$$
解答:
解答:$$此題相當於求x+y+z=20,且符合1\le x,y,z\le 12的整數解個數\\ \begin{array}{c|c|}x & y,z & 個數\\\hline 12 & y+z=8 & H^2_6\\ 11 & y+z=7& H^2_7\\ \cdots & \cdots &\cdots\\ 7& y+z=13& H^2_{11}\\\hdashline 6& y+z=14&(12,2),(11,3),\dots,(2,12),11種\\ 5&y+z=15& (12,3),\dots,(3,12),10種\\ \cdots & \cdots &\cdots \\ 1& y+z=19& (12,7),\dots, (7,12),6種\end{array} \\ 因此共有 \sum_{k=6}^{11} (H^2_k +k) =\sum_{k=6}^{11} (2k+1) =102+6= \bbox[red, 2pt]{108}$$
解答:
$$\sqrt{(x-3-2\sin y)^2+ (x^2-2\cos y)^2} =\overline{PQ}, 其中\cases{P(x^2,x-3)\\ Q(2\cos y,2\sin y)} \\ \Rightarrow \cases{P\in 拋物線:x=(y+3)^2\\ Q\in 圓:x^2+y^2=4} \Rightarrow 圓心O(0,0)至P的距離=\sqrt{x^4+x^2-6x+9} \\取f(x)=x^4+x^2-6x+9 \Rightarrow f'(x)=0 \Rightarrow 2x^3+x-3=0 \Rightarrow x=1 \Rightarrow P(1,-2) \\ \Rightarrow \overline{PQ}最小值=\overline{OP}-圓半徑=\bbox[red, 2pt]{\sqrt 5-2}$$
解答:$$令\cases{a=6\sqrt 3-10\\ b= 6\sqrt 3+10\\ k=a^{1/3}-b^{1/3}} \Rightarrow \cases{a-b=-20\\ ab= 8}\\ \Rightarrow (\sqrt[3]{6\sqrt 3-10}-\sqrt[3]{6\sqrt 3+10})^3 = (a^{1/3}-b^{1/3})^3=a-b-3(ab)^{1/3}(a^{1/3}-b^{1/3}) \\ \Rightarrow k^3=-20-6k \Rightarrow k^3+6k+20=0 \Rightarrow (k+2)(k^2-2k+10)=0 \Rightarrow k=\bbox[red, 2pt]{-2}$$
解答:$$\cases{A(3,2,1)在平面x-y-2z=5的投影點A'(4,1,-1)\\ B(2,-1,5)在平面x-y-2z=5的投影點B'(4,-3,1)} \Rightarrow P=\overline{A'B"}中點=\bbox[red, 2pt]{(4,-1,0)}$$
解答:$$有異於(0,0,0)的解代表有無限多解\Rightarrow \begin{vmatrix}\sqrt 5(\sin \theta-\cos \theta) & 2 & 1 \\3 & 1& 2\\ 21& 4 & \sqrt 5(\sin \theta-\cos \theta)+14 \end{vmatrix}=0 \\ \Rightarrow (\sin \theta-\cos \theta)^2={9\over 5} \Rightarrow \sin \theta-\cos \theta=-{3\over \sqrt 5} \;(\because -{\pi\over 4}\le \theta\le {\pi\over 4}) \\ \Rightarrow \cases{-3x+2y+z=0\\ 3x+y+2z=0\\ 21x+4y+11z=0} \Rightarrow \begin{bmatrix}-3 & 2& 1\\ 3 & 1& 2 \\21 & 4& 11 \end{bmatrix} \begin{bmatrix}x \\ y\\ z \end{bmatrix} =0 \\ 令A= \begin{bmatrix}-3 & 2& 1\\ 3 & 1& 2 \\21 & 4& 11 \end{bmatrix} \Rightarrow rref(A)= \left[\begin{matrix}1 & 0 & \frac{1}{3}\\0 & 1 & 1\\0 & 0 & 0\end{matrix}\right] \Rightarrow\cases{x+z/3=0\\ y+z=0} \Rightarrow \bbox[red, 2pt]{ \cases{x=t\\ y=3t\\ z=-3t},t\in \mathbb R}$$
解答:$$f(x)=(1+3x)^8=\sum_{k=0}^8 a_kx^k \Rightarrow a_1=C^8_1\cdot 3=24\\ f'(x)=24(1+3x)^7 =\sum_{k=1}^8k a_kx^k \Rightarrow f'(1)=24\cdot 4^7= \sum_{k=1}^8 ka_k \Rightarrow \sum_{k=2}^8 ka_k=24\cdot 4^7-a_1 \\=24\cdot 4^7-24=24(4^7-1)=\bbox[red, 2pt]{393192}$$
解答:$$令\cases{u=x+2y-z\\ v=4x-7y-5z\\ w=2x-y+3z} \Rightarrow{\partial (u,v,w)\over \partial (x,y,z)} =\begin{Vmatrix}1& 2& -1\\ 4& -7 &-5\\ 2& -1& 3 \end{Vmatrix} =80 \\ \Rightarrow \Omega={\partial (x,y,z)\over \partial (u,v,w)} \int_{-\sqrt 6}^{7\sqrt 6} \int_{-2\sqrt 2}^{6\sqrt 2} \int_{2\sqrt 3}^{5\sqrt 3}1,\,dudvdw ={1\over 80}\cdot 3\sqrt 3\cdot 8\sqrt 2\cdot 8\sqrt 6 =\bbox[red, 2pt]{72\over 5}$$
解答:$$S=\sum_{k=0}^\infty {k\over 2^k} =2\sum_{k=0}^\infty {k\over 2^{k+1}} =2\sum_{k=1}^\infty {k-1\over 2^{k}} =2\sum_{k=1}^\infty {k\over 2^{k}}-2 \sum_{k=1}^\infty {1\over 2^{k}} =2S-2 \Rightarrow S=2\\ T=\sum_{k=0}^\infty {k^2\over 2^k} =2\sum_{k=0}^\infty {k^2\over 2^{k+1}} = 2\sum_{k=1}^\infty {(k-1)^2\over 2^{k}} =2\sum_{k=1}^\infty {k^2\over 2^k}-4\sum_{k=1}^\infty{k\over 2^k}+2 \sum_{k=1}^\infty{1\over 2^k} \\\qquad =2T-4S+2 =2T-6 \Rightarrow T=6\\ U=\sum_{k=0}^\infty {k^3\over 2^k} = 2\sum_{k=0}^\infty {k^3\over 2^{k+1}} = 2\sum_{k=1}^\infty {(k-1)^3\over 2^{k}} = 2\sum_{k=1}^\infty {k^3-3k^2+3k-1\over 2^{k}} \\\qquad = 2U-6T+6S-2 =2U-36+12-2 \Rightarrow U=26 \\ \lim_{n\to \infty} \sum_{k=1}^n {a_k\over b_k} =\sum_{k=1}^\infty {k^3+k\over 3\times 2^{k-1}} ={2\over 3}\sum_{k=1}^\infty{k^3+k\over 2^k}= {2\over 3}(U+S) =\bbox[red, 2pt]{56\over 3}$$
解答:$${1\over C^{10}_4}\sum_{y=2}^8 (10-y)(y-1)C^{10-y}_2 ={1176\over 210 } = \bbox[red, 2pt]{28\over 5}$$
解答:$$令\cases{a=6\sqrt 3-10\\ b= 6\sqrt 3+10\\ k=a^{1/3}-b^{1/3}} \Rightarrow \cases{a-b=-20\\ ab= 8}\\ \Rightarrow (\sqrt[3]{6\sqrt 3-10}-\sqrt[3]{6\sqrt 3+10})^3 = (a^{1/3}-b^{1/3})^3=a-b-3(ab)^{1/3}(a^{1/3}-b^{1/3}) \\ \Rightarrow k^3=-20-6k \Rightarrow k^3+6k+20=0 \Rightarrow (k+2)(k^2-2k+10)=0 \Rightarrow k=\bbox[red, 2pt]{-2}$$
解答:$$\cases{A(3,2,1)在平面x-y-2z=5的投影點A'(4,1,-1)\\ B(2,-1,5)在平面x-y-2z=5的投影點B'(4,-3,1)} \Rightarrow P=\overline{A'B"}中點=\bbox[red, 2pt]{(4,-1,0)}$$
解答:$$有異於(0,0,0)的解代表有無限多解\Rightarrow \begin{vmatrix}\sqrt 5(\sin \theta-\cos \theta) & 2 & 1 \\3 & 1& 2\\ 21& 4 & \sqrt 5(\sin \theta-\cos \theta)+14 \end{vmatrix}=0 \\ \Rightarrow (\sin \theta-\cos \theta)^2={9\over 5} \Rightarrow \sin \theta-\cos \theta=-{3\over \sqrt 5} \;(\because -{\pi\over 4}\le \theta\le {\pi\over 4}) \\ \Rightarrow \cases{-3x+2y+z=0\\ 3x+y+2z=0\\ 21x+4y+11z=0} \Rightarrow \begin{bmatrix}-3 & 2& 1\\ 3 & 1& 2 \\21 & 4& 11 \end{bmatrix} \begin{bmatrix}x \\ y\\ z \end{bmatrix} =0 \\ 令A= \begin{bmatrix}-3 & 2& 1\\ 3 & 1& 2 \\21 & 4& 11 \end{bmatrix} \Rightarrow rref(A)= \left[\begin{matrix}1 & 0 & \frac{1}{3}\\0 & 1 & 1\\0 & 0 & 0\end{matrix}\right] \Rightarrow\cases{x+z/3=0\\ y+z=0} \Rightarrow \bbox[red, 2pt]{ \cases{x=t\\ y=3t\\ z=-3t},t\in \mathbb R}$$
解答:$$f(x)=(1+3x)^8=\sum_{k=0}^8 a_kx^k \Rightarrow a_1=C^8_1\cdot 3=24\\ f'(x)=24(1+3x)^7 =\sum_{k=1}^8k a_kx^k \Rightarrow f'(1)=24\cdot 4^7= \sum_{k=1}^8 ka_k \Rightarrow \sum_{k=2}^8 ka_k=24\cdot 4^7-a_1 \\=24\cdot 4^7-24=24(4^7-1)=\bbox[red, 2pt]{393192}$$
解答:$$令\cases{u=x+2y-z\\ v=4x-7y-5z\\ w=2x-y+3z} \Rightarrow{\partial (u,v,w)\over \partial (x,y,z)} =\begin{Vmatrix}1& 2& -1\\ 4& -7 &-5\\ 2& -1& 3 \end{Vmatrix} =80 \\ \Rightarrow \Omega={\partial (x,y,z)\over \partial (u,v,w)} \int_{-\sqrt 6}^{7\sqrt 6} \int_{-2\sqrt 2}^{6\sqrt 2} \int_{2\sqrt 3}^{5\sqrt 3}1,\,dudvdw ={1\over 80}\cdot 3\sqrt 3\cdot 8\sqrt 2\cdot 8\sqrt 6 =\bbox[red, 2pt]{72\over 5}$$
解答:$$S=\sum_{k=0}^\infty {k\over 2^k} =2\sum_{k=0}^\infty {k\over 2^{k+1}} =2\sum_{k=1}^\infty {k-1\over 2^{k}} =2\sum_{k=1}^\infty {k\over 2^{k}}-2 \sum_{k=1}^\infty {1\over 2^{k}} =2S-2 \Rightarrow S=2\\ T=\sum_{k=0}^\infty {k^2\over 2^k} =2\sum_{k=0}^\infty {k^2\over 2^{k+1}} = 2\sum_{k=1}^\infty {(k-1)^2\over 2^{k}} =2\sum_{k=1}^\infty {k^2\over 2^k}-4\sum_{k=1}^\infty{k\over 2^k}+2 \sum_{k=1}^\infty{1\over 2^k} \\\qquad =2T-4S+2 =2T-6 \Rightarrow T=6\\ U=\sum_{k=0}^\infty {k^3\over 2^k} = 2\sum_{k=0}^\infty {k^3\over 2^{k+1}} = 2\sum_{k=1}^\infty {(k-1)^3\over 2^{k}} = 2\sum_{k=1}^\infty {k^3-3k^2+3k-1\over 2^{k}} \\\qquad = 2U-6T+6S-2 =2U-36+12-2 \Rightarrow U=26 \\ \lim_{n\to \infty} \sum_{k=1}^n {a_k\over b_k} =\sum_{k=1}^\infty {k^3+k\over 3\times 2^{k-1}} ={2\over 3}\sum_{k=1}^\infty{k^3+k\over 2^k}= {2\over 3}(U+S) =\bbox[red, 2pt]{56\over 3}$$
解答:$${1\over C^{10}_4}\sum_{y=2}^8 (10-y)(y-1)C^{10-y}_2 ={1176\over 210 } = \bbox[red, 2pt]{28\over 5}$$
解答:$$假設\cases{\overline{AD}=a\\ \overline{AB}=a+\sqrt{11}\\ \overline{BC}=b\\ \overline{CD}=\sqrt{13}-b} \Rightarrow \overline{AC}^2=\overline{AB}^2+\overline{BC}^2= \overline{AD}^2+ \overline{CD}^2 \\ \Rightarrow 16= a^2 +2\sqrt{11}a+11+b^2= a^2+b^2-2\sqrt{13} b+13 \Rightarrow \sqrt{11}a+ \sqrt{13}b=1 \\ \Rightarrow a={1-\sqrt{13}b\over \sqrt{11}} \Rightarrow ({1-\sqrt{13}b\over \sqrt{11}})^2+b^2-2\sqrt{13} b+13=16 \Rightarrow b={3\sqrt{13}-\sqrt{165} \over 6}\\ 又\overline{AC}\times \overline{BD}= \overline{AB}\cdot \overline{CD}+ \overline{BC}\cdot \overline{AD} \\ \Rightarrow 4\overline{BD}=\sqrt{13}a-\sqrt{11}b+\sqrt{143} \Rightarrow \overline{BD}={1\over 4}(\sqrt{13}a-\sqrt{11}b+\sqrt{143}) \\ ={3\sqrt{13}-6b\over \sqrt{11}} ={\sqrt{165}\over \sqrt{11}} =\bbox[red, 2pt]{\sqrt{15}}$$










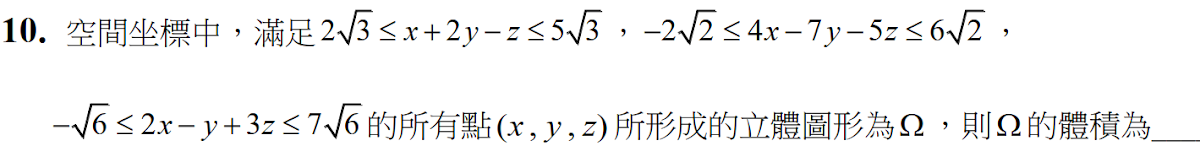






























填充第13題是不是有問題啊? 因為b=(3√13−√165)/6<0,但b必須>0.(ps:b=(3√13+√165)/6 也不行,試算過了)
回覆刪除作者已經移除這則留言。
刪除也許四邊形的順序不是ABCD,而是ACBD,這樣結果就符合運算結果!
刪除可是他有說四邊形ABCD喔,所以明確題目有誤(這題其他論壇也有人討論).
刪除