臺灣警察專科學校113學年度專科警員班第43期
正期學生組新生入學考試-乙組數學科
解答:$$\sqrt{14+8\sqrt 3}+\sqrt{14-8\sqrt 3} =\sqrt{14+2\sqrt {48}}+\sqrt{14-2\sqrt {48}} =\sqrt 8+\sqrt 6+\sqrt 8-\sqrt 6 \\=2\sqrt 8=4\sqrt 2，故選\bbox[red, 2pt]{(C)}$$
解答:$$100\le (1.5)^n \le 500 \Rightarrow 2\le n\log 1.5\le 2+\log 5\Rightarrow 2\le n(\log 3-\log 2)\le 2+(1-\log 2) \\ \Rightarrow {2\over \log 3-\log 2}\le n\le {3-\log 2\over \log 3-\log 2} \Rightarrow {2\over 0.4771-0.301} \le n\le {3-0.301\over 0.4771-0.301} \\ \Rightarrow 11.36\le n\le 15.33 \Rightarrow n=12,13,14,15,共四個，故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{A(2,\log 2)\\ B(3,\log 3) \\ C(6,\log a)} \Rightarrow \cases{\overrightarrow{AB}=(1,\log 3-\log 2)\\ \overrightarrow{AC}= (4,\log a-\log 2)} \Rightarrow \overrightarrow{AB} \parallel \overrightarrow{AC} \Rightarrow {1\over 4}={\log 3-\log 2\over \log a-\log 2} \\ \Rightarrow 4\log 3-4\log 2=\log a-\log 2 \Rightarrow \log a=4\log 3-3\log 2= \log {3^4\over 2^3} =\log {81\over 8} \\ \Rightarrow a={81\over 8}，故選\bbox[red, 2pt]{(D)}$$
解答:$$\overline{BD}=6 \Rightarrow \overline{CD}=2 \Rightarrow \cases{\cos \angle ADB={36+\overline{AD}^2-49\over 12\overline{AD}} \\ \cos \angle ADC={4+\overline{AD}^2-25\over 4\overline{AD}}} \Rightarrow \cos \angle ADB=-\cos \angle ADC \\ \Rightarrow {\overline{AD}^2-13\over 12\overline{AD}}=-{\overline{AD}^2-21\over 4\overline{AD}} \Rightarrow \overline{AD}^2-13 =-3(\overline{AD}^2-21) \Rightarrow 4\overline{AD}^2= 76 \\ \Rightarrow \overline{AD}=\sqrt{19}，故選\bbox[red, 2pt]{(A)}$$
解答:$$A=\begin{bmatrix}a & 0 \\0 & b \end{bmatrix} \Rightarrow A^2=\begin{bmatrix}a^2 & 0 \\0 & b^2 \end{bmatrix} =\begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix} \Rightarrow \cases{a=\pm 1\\b=\pm 1} \Rightarrow 共2\times 2=4個，故選\bbox[red, 2pt]{(C)}$$
解答:$$本題\bbox[cyan, 2pt]{送分}$$
解答:$$(1,2,8),(1,4,9),(2,3,6) ,(2,4,8),(2,8,9),(3,6,8),共六組，故選\bbox[red, 2pt]{(D)}$$
解答:$$AB= \begin{bmatrix}2 & 0 \\0 & 2 \end{bmatrix} =2I \Rightarrow {1\over 2}AB=I \Rightarrow B=({1\over 2}A)^{-1}= \begin{bmatrix}1/2 & 1 \\3/2 & 2 \end{bmatrix}^{-1}= \begin{bmatrix}-4 & 2 \\3 & -1 \end{bmatrix} \\\Rightarrow a+b+c+ d =-4+2+3-1=0，故選\bbox[red, 2pt]{(A)}$$
解答:$$(1-(-2))(1-(-1))\times 4\times 2=3\times 2 \times 4 \times 2=48，故選\bbox[red, 2pt]{(D)}$$
解答:$$1-15有\cases{7個偶數\\ 8個奇數} \Rightarrow \cases{三偶=C^7_3 =35\\ 二奇一偶=C^8_2C^7_1=196} \Rightarrow 35+196=231，故選\bbox[red, 2pt]{(D)}$$
解答:$$y=f(x)=ax^2+(a+1)x+2a-1 \gt 0 \Rightarrow a\gt 0且判別式:(a+1)^2-4a(2a-1)\lt 0 \\ \Rightarrow (7a+1)(a-1)\gt 0 \Rightarrow a\gt 1，故選\bbox[red, 2pt]{(D)}$$
解答:$${4\times 3\times 2\times 3!\over 9\times 8\times 7} ={2\over 7}，故選\bbox[red, 2pt]{(B)}$$
解答:$$假設未摺起前\cases{O(0,0,0)\\ A(-1,1,0)\\ B(1,1,0)\\ C(1,-1,0)\\ D(-1,-1,0)},B,C,D不動,沿著\overline{BD}將A摺起至A',使得\angle A'OC=60^\circ\\ \Rightarrow A'({1\over 2},-{1\over 2},{\sqrt 6\over 2}) \Rightarrow \cases{\overrightarrow{BA'}=(-{1\over 2},-{3\over 2},{\sqrt 6\over 2}) \\ \overrightarrow{BC}=(0,-2,0)} \Rightarrow \cos \theta={\overrightarrow{BA'} \cdot \overrightarrow{BC} \over |\overrightarrow{BA'} ||\overrightarrow{BC}|} ={3\over 2\cdot 2} ={3\over 4}，故選\bbox[red, 2pt]{(C)}$$
解答:$${陽性且罹病\over 陽性} ={6\%\times 90\%\over 94\%\times 5\%+ 6\%\times 90\%} ={540\over 1010} ={54\over 101}，故選\bbox[red, 2pt]{(D)}$$
解答:$$(x+2)^2+(y-1)^2=10 \Rightarrow 2(x+2)+2(y-1)y'=0 \Rightarrow y'={x+2\over 1-y} \\ \Rightarrow y'(1,0)=3 \Rightarrow L: y=3(x-1) \Rightarrow 3x-y=3 \Rightarrow \cases{L與x軸交於A(1,0)\\ L與y軸交於B(0,-3)} \\ \Rightarrow \triangle OAB面積={1\over 2}\cdot 1\cdot 3={3\over 2}，故選\bbox[red, 2pt]{(B)}$$
解答:$$本題\bbox[cyan, 2pt]{送分}$$
解答:$${1\over 1},\left({1\over 2},{2\over 1} \right),\left({1\over 3},{2\over 2},{3\over 1} \right), \dots,\left({1\over 19},{2\over 18},{3\over 17},\dots,{7\over 13},\dots,{19\over 1} \right) \\ \Rightarrow 1+2+\cdots+18=171 \Rightarrow {7\over 13}在第171+7=178項，故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{(A) \sin{\pi\over 6}=\sin 30^\circ={1\over 2}\\ (B) \cos{\pi\over 5}=\cos 36^\circ=\sin 54^\circ \gt \sin 30^\circ\\ (C) \sin 1=\sin {180^\circ\over \pi} =\sin 57^\circ \gt \sin 54^\circ\\ (D) \sin 2=\sin 114.6 =\sin 65.4^\circ } \Rightarrow (D)\gt (C)\gt (B)\gt (A)，故選\bbox[red, 2pt]{(D)}$$
解答:$$C^{20}_0+ 3C^{20}_1+9C^{20}_2+\cdots +3^{20}C^{20}_{20} =(1+3)^{20}=4^{20} \Rightarrow \log 4^{20}=40\log 2=12.04\\ \Rightarrow 12+1=13位數數，故選\bbox[red, 2pt]{(C)}$$
解答:$$本題\bbox[cyan, 2pt]{送分}$$
解答:$$假設\cases{\langle a_n\rangle 首項a,公差d\\ \langle b_n\rangle 首項b,公差s} \Rightarrow f(n)={S_n\over T_n}={2a+(n-1)d\over 2b+(n-1)s} ={7n+3\over 2n+5} \\ \Rightarrow {a_2+a_{10}\over b_2+b_{10}} ={2a+10d\over 2b+10s} =f(11)={80\over 27}，故選\bbox[red, 2pt]{(B)}$$
解答:$$P在x^2+y^2=4上 \Rightarrow P(2\cos \theta, 2\sin \theta) \Rightarrow \cases{\overrightarrow{PA} =(-2\cos\theta,4-2\sin \theta) \\ \overrightarrow{PB}= (4\sqrt 3-2\cos \theta,-2\sin \theta)} \\ \Rightarrow \overrightarrow{PA} \cdot \overrightarrow{PB} =-8\sqrt 3 \cos \theta+4\cos^2\theta-8\sin \theta+4\sin^2\theta =4-8(\sqrt 3\cos \theta+\sin \theta) \\=4-16({\sqrt 3\over 2}\cos \theta+ {1\over 2}\sin \theta)=4-16\sin(60^\circ+\theta) 最大值=4+16=20，故選\bbox[red, 2pt]{(A)}$$
解答:$${4^t\over 2^t}=512 \Rightarrow 2^t=2^9 \Rightarrow t=9，故選\bbox[red, 2pt]{(C)}$$
解答:$$本題\bbox[cyan, 2pt]{送分}$$
解答:$$\cases{水平切 \Rightarrow 圓形\\垂直切 \Rightarrow 長方形\\ 斜角切 \Rightarrow 橢圓形} \Rightarrow 不可能雙曲線，故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{D(0,0,0)\\ A(0,0,2)\\ B(-4,0,0)\\ C(0,4,0)} \Rightarrow \cases{P=(A+D)\div 2=(0,0,1)\\ Q=(B+C)\div 2=(-2,2,0)} \Rightarrow \overline{PQ}=\sqrt{4+4+1}=3，故選\bbox[red, 2pt]{(B)}$$
解答:$$\cases{甲乙中,丙不中\Rightarrow 機率=0.6\cdot 0.7\cdot (1-0.5)=0.21 \\甲丙中,乙不中 \Rightarrow 機率=0.6\cdot 0.5\cdot (1-0.7) =0.09\\ 乙丙中,甲不中 \Rightarrow 機率=0.7\cdot 0.5\cdot (1-0.6) =0.14} \\ \Rightarrow 0.21+0.09+0.14=0.44，故選\bbox[red, 2pt]{(C)}$$
解答:$$\cases{x=\sqrt{6+\sqrt{20}} \\ y=\sqrt{6-\sqrt{20}}} \Rightarrow \cases{x^2+y^2=12\\ xy=4} \Rightarrow (x-y)^2=x^2+y^2-2xy=12-8=4 \Rightarrow x-y=2\\ \Rightarrow x^3-y^3=(x-y)(x^2+xy+y^3) =2(12+4)=32，故選\bbox[red, 2pt]{(C)}$$
解答:$$\tan 140^\circ= -\tan 40^\circ =k \Rightarrow \tan 40^\circ=-k \Rightarrow \cos 40^\circ ={1\over \sqrt{1+k^2}}\\ \Rightarrow \sin 230^\circ= -\sin 50^\circ= -\cos 40^\circ=-{1\over \sqrt{1+k^2}}，故選\bbox[red, 2pt]{(B)}$$
解答:$$半徑R=6370\cos 30^\circ={6370 \over 2}\sqrt 3 \Rightarrow 直徑2R= 6370\sqrt 3，故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{A[2,130^\circ]= (2\cos 130^\circ, 2\sin 130^\circ)\\ B[4,220^\circ] = (4\cos 220, 4\sin 220^\circ)} \Rightarrow C\left({2\cos 130^\circ+ 4\cos 220^\circ\over 2},{2\sin 130^\circ+ 4\sin 220^\circ \over 2} \right) \\=(\cos 130^\circ+2\cos220^\circ ,\sin 130^\circ+2\sin 220^\circ) \\\Rightarrow \overline{OC} =\sqrt{(\cos 130^\circ+2\cos220^\circ)^2+ (\sin 130^\circ+2\sin 220^\circ)^2} \\= \sqrt{5+4(\cos 220^\circ \cos 130^\circ+ \sin220^\circ \sin 130^\circ)} =\sqrt{5+4\cos(220^\circ-130^\circ)} =\sqrt 5，故選\bbox[red, 2pt]{(C)}$$
解答:
$$(2,0)是對稱中心,因此f(0)=0 \Rightarrow f(4)=0,又f(-3)\gt 0\\ 因此圖形為左上右下,且f(0)=f(2)=f(4)=0 \Rightarrow f(x)\gt 0, \text{if }x\lt 0,x\in(2,4)\\ 因此f(-2),f(3)大於0，故選\bbox[red, 2pt]{(A)}$$
解答:$$(x,y)=(2,-2),(1,-3),(2,-3),(3,-4), (1,-4),(2,-4),(3,-4), (4,-4),\\ \qquad (1,-5),(2,-5),(3,-5), (4,-5),(5,-5),(2,-6),(3,-6),(4,-6)\\ 共16個格子點，故選\bbox[red, 2pt]{(B)}$$
解答:$$繩子擺成ㄇ字形,左右兩邊為河寬長度x, 上方長度=20-2x \Rightarrow 面積=f(x)=x(20-2x)\\ \Rightarrow f'(x)=20-4x=0 \Rightarrow x=5 \Rightarrow f(5)=5\cdot 10=50，故選\bbox[red, 2pt]{(D)}$$
解答:$$本題\bbox[cyan, 2pt]{送分}$$
解答:$$最適直線方程式:y=mx+b \Rightarrow m=r\cdot {\sigma_y\over \sigma_x} =0.8\cdot {5\over 10}=0.4 \\ 該直線通過(\mu_x,\mu_y)=(65,70) \Rightarrow 70=0.4\cdot 65+b \Rightarrow b=44 \Rightarrow y=0.4x+44\\ x=70代入直線方程式\Rightarrow y=0.4\cdot 70+44=72，故選\bbox[red, 2pt]{(C)}$$
解答:$$A=\begin{bmatrix}a & b \\c & d \end{bmatrix} \Rightarrow \cases{A\begin{bmatrix}1 \\-1 \end{bmatrix} =\begin{bmatrix}a-b \\c-d \end{bmatrix}=\begin{bmatrix}1 \\1 \end{bmatrix} \\[1ex]A\begin{bmatrix}1 \\1 \end{bmatrix} =\begin{bmatrix}a+b \\c+d \end{bmatrix} =\begin{bmatrix}-1 \\ 1 \end{bmatrix}} \Rightarrow \cases{\cases{a-b=1\\ a+b=-1} \\\cases{c-d=1\\ c+d=1}} \\ \Rightarrow \cases{a=0\\ b=-1\\ c=1\\ d=0} \Rightarrow A=\begin{bmatrix}0 & -1 \\1 & 0 \end{bmatrix} \Rightarrow A^2=\begin{bmatrix}-1 & 0 \\0 & -1 \end{bmatrix} \Rightarrow A^3=\begin{bmatrix}0 &1 \\-1 & 0 \end{bmatrix}，故選\bbox[red, 2pt]{(A)}$$
解答:$$沿著\overline{EF}將\overline{HG}往上攤平,使得ABFGHE成為一個平面,\\ \overline{AG}^2=\overline{AB}^2+(\overline{BF}+\overline{FG})^2 =4^2+5^2=41\Rightarrow \overline{AG}=\sqrt{41}，故選\bbox[red, 2pt]{(C)}$$
解答:
$$\cases{A(3,4)\\ O(0,0)} \Rightarrow 圓半徑r=\overline{OA}=5, 又\triangle ABC為正三角形\Rightarrow \angle AOB=2\angle C=120^\circ \\ \Rightarrow \cos \angle AOB=-{1\over 2}={5^2+5^2-\overline{AB}^2 \over 2\cdot 5\cdot 5} \Rightarrow \overline{AB}^2= 75 \Rightarrow \triangle ABC面積={\sqrt 3\over 4}\cdot \overline{AB}^2\\={75\sqrt 3\over 4} ，故選\bbox[red, 2pt]{(C)}$$
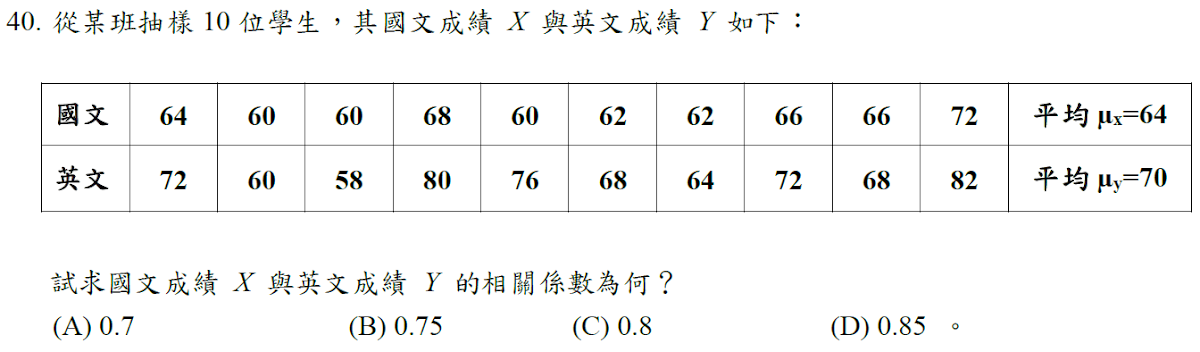
解答:$$\begin{array}{ccc |rrrrr}&X & Y& X-\mu_X & Y-\mu_Y& (X-\mu_X)^2 & (Y-\mu_Y)^2 &(X-\mu_X)( Y-\mu_Y)\\\hline & 64&72& 0 & 2& 0 & 4&0\\ & 60& 60 & -4& -10& 16&100& 40\\ &60& 58 & -4& -12& 16& 144&48\\ & 68& 80& 4& 10&16 & 100& 40\\ & 60& 76& -4& 6& 16& 36& -24\\ & 62&68& -2& -2& 4& 4& 4\\ & 62& 64& -2& -6& 4& 36& 12\\ & 66& 72 & 2& 2 & 4& 4& 4\\ & 66& 68 & 2& -2&4& 4& -4\\ & 72& 82& 8& 12&64& 144& 96\\\hline \sum & & & & & 144& 576& 216 \end{array}\\ \Rightarrow 相關係數r={\sum(x-\mu_x)(y-\mu_y) \over \sqrt{\sum(x-\mu_x)^2}\cdot \sqrt{\sum(y-\mu_y)^2}} ={216\over \sqrt{144}\cdot\sqrt {576}} ={216\over 12\cdot 24} ={3\over 4}=0.75，故選\bbox[red, 2pt]{(B)}$$
=================== END ====================
解題僅供參考,警專歷年試題及詳解
解答:$$(x,y)=(2,-2),(1,-3),(2,-3),(3,-4), (1,-4),(2,-4),(3,-4), (4,-4),\\ \qquad (1,-5),(2,-5),(3,-5), (4,-5),(5,-5),(2,-6),(3,-6),(4,-6)\\ 共16個格子點，故選\bbox[red, 2pt]{(B)}$$
解答:$$繩子擺成ㄇ字形,左右兩邊為河寬長度x, 上方長度=20-2x \Rightarrow 面積=f(x)=x(20-2x)\\ \Rightarrow f'(x)=20-4x=0 \Rightarrow x=5 \Rightarrow f(5)=5\cdot 10=50，故選\bbox[red, 2pt]{(D)}$$
解答:$$本題\bbox[cyan, 2pt]{送分}$$
解答:$$最適直線方程式:y=mx+b \Rightarrow m=r\cdot {\sigma_y\over \sigma_x} =0.8\cdot {5\over 10}=0.4 \\ 該直線通過(\mu_x,\mu_y)=(65,70) \Rightarrow 70=0.4\cdot 65+b \Rightarrow b=44 \Rightarrow y=0.4x+44\\ x=70代入直線方程式\Rightarrow y=0.4\cdot 70+44=72，故選\bbox[red, 2pt]{(C)}$$
解答:$$A=\begin{bmatrix}a & b \\c & d \end{bmatrix} \Rightarrow \cases{A\begin{bmatrix}1 \\-1 \end{bmatrix} =\begin{bmatrix}a-b \\c-d \end{bmatrix}=\begin{bmatrix}1 \\1 \end{bmatrix} \\[1ex]A\begin{bmatrix}1 \\1 \end{bmatrix} =\begin{bmatrix}a+b \\c+d \end{bmatrix} =\begin{bmatrix}-1 \\ 1 \end{bmatrix}} \Rightarrow \cases{\cases{a-b=1\\ a+b=-1} \\\cases{c-d=1\\ c+d=1}} \\ \Rightarrow \cases{a=0\\ b=-1\\ c=1\\ d=0} \Rightarrow A=\begin{bmatrix}0 & -1 \\1 & 0 \end{bmatrix} \Rightarrow A^2=\begin{bmatrix}-1 & 0 \\0 & -1 \end{bmatrix} \Rightarrow A^3=\begin{bmatrix}0 &1 \\-1 & 0 \end{bmatrix}，故選\bbox[red, 2pt]{(A)}$$
解答:$$沿著\overline{EF}將\overline{HG}往上攤平,使得ABFGHE成為一個平面,\\ \overline{AG}^2=\overline{AB}^2+(\overline{BF}+\overline{FG})^2 =4^2+5^2=41\Rightarrow \overline{AG}=\sqrt{41}，故選\bbox[red, 2pt]{(C)}$$
解答:
解答:$$\begin{array}{ccc |rrrrr}&X & Y& X-\mu_X & Y-\mu_Y& (X-\mu_X)^2 & (Y-\mu_Y)^2 &(X-\mu_X)( Y-\mu_Y)\\\hline & 64&72& 0 & 2& 0 & 4&0\\ & 60& 60 & -4& -10& 16&100& 40\\ &60& 58 & -4& -12& 16& 144&48\\ & 68& 80& 4& 10&16 & 100& 40\\ & 60& 76& -4& 6& 16& 36& -24\\ & 62&68& -2& -2& 4& 4& 4\\ & 62& 64& -2& -6& 4& 36& 12\\ & 66& 72 & 2& 2 & 4& 4& 4\\ & 66& 68 & 2& -2&4& 4& -4\\ & 72& 82& 8& 12&64& 144& 96\\\hline \sum & & & & & 144& 576& 216 \end{array}\\ \Rightarrow 相關係數r={\sum(x-\mu_x)(y-\mu_y) \over \sqrt{\sum(x-\mu_x)^2}\cdot \sqrt{\sum(y-\mu_y)^2}} ={216\over \sqrt{144}\cdot\sqrt {576}} ={216\over 12\cdot 24} ={3\over 4}=0.75，故選\bbox[red, 2pt]{(B)}$$
沒有留言:
張貼留言