113年大學學測-數學B詳解

113學年度學科能力測驗試題 數學B考科

 壹 部分 、選 擇（填） 題 （占 85分 ）
一 、單選 題（ 占 35分）

解答: $$210\times 90\%= 189\\ \sum_{k=1}^{16} k={16\cdot 17 \over 2} =136 \Rightarrow \sum_{k=1}^{17} k= 136+17=153 \Rightarrow \sum_{k=1}^{18} k= 153+18=171 \\ \Rightarrow \sum_{k=1}^{19} k=171+19=190 \ge 189, 故選\bbox[red, 2pt]{(4)}$$

解答: $$1\lt a\lt 10 \Rightarrow \log 1\lt b=\log a\lt \log 10 \Rightarrow 0\lt b\lt 1 \Rightarrow c=\log b\lt \log 1 \\ \Rightarrow c\lt 0 \Rightarrow c\lt 0\lt b\lt 1, 故選\bbox[red, 2pt]{(1)}$$

解答: $$假設Q(x,y), 由於\cases{Q在D的左邊\Rightarrow x\lt 9\\ Q在A的下方 \Rightarrow y\lt 5} \Rightarrow 僅需考慮選項(1)及(2)\\ 若Q=(6,3) \Rightarrow L=\overleftrightarrow{PQ}:y=7x/6-4 與水平線: y=6交於(8.5,6)在D的左邊 \\ \Rightarrow \overline{PQ}與\overline{CD}有交點,違反題意, 故選\bbox[red, 2pt]{(2)}$$

解答: $$假設\overrightarrow{AB}=(a,b), -1\le a,b\le 1 \Rightarrow |\vec v+\overrightarrow{AB}| =|(a-2,b+3)| 要最大 \Rightarrow 取\cases{a=-1\\b=1} \\ \Rightarrow |\vec v+\overrightarrow{AB}|=|(-3,4)| =\sqrt{25}=5, 故選\bbox[red, 2pt]{(4)}$$

解答: $$f(x-2)=f(-x-2) \Rightarrow (x-2)^2+b(x-2)+c= (-x-2)^2+b(-x-2)+c\\ \Rightarrow x^2+(b-4)x+4-2b+c=x^2+(4-b)x+4-2b+c \Rightarrow b-4=4-b\\ \Rightarrow b=4 \Rightarrow f(x)=x^2+4x+c =(x+2)^2+c-4 \Rightarrow \cases{最小值f(-2)\\ 最大值f(1)} \\又最大值是最小值的4倍 \Rightarrow f(1)=4f(-2) \Rightarrow 5+c=4(c-4) \Rightarrow c=7\\ \Rightarrow 最小值=f(-2)=c-4=7-4=3, 故選\bbox[red, 2pt]{(3)}$$

解答:

$$假設\cases{樓地板長度=w\\ 樓層高度=h\\ E(0,0)} \Rightarrow \cases{P({w\over 2},3.5h)\\ A(0,2h)\\ \overline{GH}:y=3h} \Rightarrow   \overline{PE}:y={7h\over w}x\\ \overline{PE}與y=3h交於R({3w\over 7},3h) \Rightarrow 欲求截出之長度=w-{3w\over 7} \times 2={1\over 7}w, 故選\bbox[red, 2pt]{(1)}$$

解答: $$東區每天氣溫都高於24度,因此該城市最高溫低於24度的天數為0,即A=0\\ 東區有5天氣溫度高於36度,而西區沒有高於36度的日子,因此D=5\\ 因此僅需考慮選項(3)與(5),也就是B+C=25\\ 若B=12,代表西區有一天氣溫介於24與30之間,該天東區氣溫需低於24,\\可是東區沒有一天氣溫低於24,因此B\ne 12, 故選\bbox[red, 2pt]{(3)}$$

二 、多選 題（占 25 分 ）

解答: $$(1): \bigcirc: \cases{a,ar,ar^2,ar^3,ar^4為公比=r的等比數列\\ a,-ar,ar^2,-ar^3,ar^4為公比=-r的等比數列} \\(2): \bigcirc: \cases{a,ar,ar^2,ar^3,ar^4為公比=r的等比數列\\ ar^4,ar^3,ar^2,ar,a為公比=1/r的等比數列} \\(3)\times: a,ar,ar^2,ar^3,ar^4為公比=r的等比數列 \Rightarrow \cases{\log a\\ \log(ar)=\log a+\log r\\ \log(ar^2)= \log a+2\log r\\ \log(ar^3)=\log a+3\log r\\ \log(ar^4) =\log a+4\log r}\\ \qquad \Rightarrow \log a,\log b,\log c,\log d,\log  e 為等差數列\\ (4)\times: a,ar,ar^2,ar^3,ar^4為公比=r的等比數列 \Rightarrow \cases{3^a\\ 3^b=3^{ar} \\ 3^c=3^{ar^2}} \Rightarrow \cases{3^b/3^a= 3^{a(r-1)} \\ 3^c/3^b =3^{ar(r-1)}} \\ \qquad \Rightarrow {3^b\over 3^a} \ne {3^c\over 3^b} \Rightarrow 非等比數列\\(5)\bigcirc:  \cases{abc= a\cdot ar\cdot ar^2= a^3r^3\\ bcd=ar\cdot ar^2\cdot ar^3 =a^3r^6 \\ cde =ar^2\cdot ar^3\cdot ar^4 =a^3r^9} \Rightarrow {bcd\over abc}=r^3={cde\over bcd} \Rightarrow 等比數列\\, 故選\bbox[red, 2pt]{(125)}$$

解答: $$(1)\times: f(x)=2(x^3+7x^2+x+3)(x^2+5x+1) \Rightarrow 商式應為2(x^3+7x^2+x+3) \\(2)\bigcirc:f(x)= (x^3+7x^2+x+3)(x^2+5x+1)-x \Rightarrow \cases{商式=x^3+7x^2+x+3\\ 餘式=-x} \\(3)\times: 除式x^2+5x+1為2次式 \Rightarrow 餘式應為一次式或常數,但x^2為二次式\\ (4)\times: f(x)=(x^3+7x^2+x+4)(x^2+5x+1)-x \Rightarrow 商式應為x^3+7x^2+x+4 \\(5) \bigcirc: f(x)=(x^3+7x^2+x+4)(x^2+5x+1)-x^2\\\qquad =(x^3+7x^2+x+3)(x^2+5x+1) +(x^2+5x+1)-x \\\qquad =(x^3+7x^2+x+3)(x^2+5x+1) +5x+1   \Rightarrow \cases{商式=x^3+7x^2+x+3\\ 餘式=5x+1}\\ , 故選\bbox[red, 2pt]{(25)}$$

解答: $$(1)\bigcirc: 假設過了s秒兩光點相遇 \Rightarrow (5+10)s=120 \Rightarrow s=8 \Rightarrow A光點走了8\cdot 5=40公分 \\(2)\times:來回240公分,週期應為240\div 5=48秒\\ (3)\bigcirc: A回到出發點花48秒,此時B走了48\times 10=480=240\times 2 \\\qquad \Rightarrow B走了來回兩趟,剛好回到出發點\\(4) \bigcirc: A花了{120\over5}=24秒從出發點走到對面端點(B的出發點),此時B走了24\times 10=240公分,\\\qquad 剛好回到B的出發點\\(5)\times:\cases{8秒\cases{A走了40\\ B走了80} \Rightarrow 相遇在離A出發點40公分\\ 24秒\cases{A走了120\\ B走了240} \Rightarrow 相遇在B的出發點\\ 40秒\cases{A走了200 \\ B走了400} \Rightarrow 相遇在離A出發點40公分\\ 48秒\cases{A走了240\\ B走了480} \Rightarrow 回到各自的出發點}\\\qquad \Rightarrow 只有兩個不同的相遇位置, 故選\bbox[red, 2pt]{(134)}$$

解答: $$((1)\bigcirc: 第2年的碳排放年成長率為-0.07 \Rightarrow A=0.93X \\(2)\times: 0.95^4=0.95^2\times 0.95^2 =0.9025\times 0.9025 \gt 0.8 \Rightarrow Y\gt 0.8X \\(3)\times: 由(5)可知該式不成立\\(4)\bigcirc: Y=(1-0.05)^4X \Rightarrow \sqrt[4]{Y\over X} =0.95 \Rightarrow \sqrt[4]{Y\over X}-1=-0.05\\ (5)\bigcirc: \cases{A=0.93X\\ B=(1+p)A\\ C=(1+q)B\\ Y= (1+r)C} \Rightarrow Y=(1+r)(1+q)(1+p)0.93X = (1-0.05)^4X \\ \qquad \Rightarrow 0.93(1+p)(1+q)(1+r)= 0.95^4\\, 故選\bbox[red, 2pt]{(145)}$$

解答: $$由棋盤可知:\cases{P(A\to A)=1/2, P(A\to B)=P(A\to C)= 1/4 \\ P(B\to B)=1/2, P(B\to A)= P(B\to D)=1/4\\ P(C\to C)=1/2, P(C\to A)=P(C\to D)=1/4\\ P(D \to D)=1/2, P(D\to B)= P(D\to C) =1/4} \\(1)\bigcirc: b_1=P(A\to B)=1/4\\ (2) \times: b_2=P(A\to A\to B)+ P(A\to B \to B)={1\over 2}\cdot {1\over 4} +{1\over 4}\cdot {1\over 2}={1\over 4} \\(3)\times: \cases{a_2=P(A\to A\to A)+ P(A\to B\to A) +P(A\to C\to A) ={1\over 4}+{1\over 16}+ {1\over 16}={3\over 8} \\ d_2= P(A\to B\to D)+ P(A\to C\to D)= {1\over 16}+{1\over 16} ={1\over 8}} \\\qquad \Rightarrow a_2+d_2={1\over 2}\\ (4)\bigcirc: B與C對稱,機率相同\\(5)\times: a_{n}+d_n=b_n+c_n ={1\over 2}\\, 故選\bbox[red, 2pt]{(14)}$$

三 、 選填 題（占 25 分 ）

解答: $$\begin{bmatrix}1 &-1 \\3 & -2 \end{bmatrix} \begin{bmatrix}a  \\b\end{bmatrix} =\begin{bmatrix}1 \\0 \end{bmatrix} \Rightarrow \cases{a-b=1\\ 3a-2b=0} \Rightarrow \cases{a=-2 \\b=-3} \\\begin{bmatrix}1 &-1 \\3 & -2 \end{bmatrix} \begin{bmatrix}2a+1  \\ 2b+1 \end{bmatrix} = \begin{bmatrix}1 &-1 \\3 & -2 \end{bmatrix} \begin{bmatrix}-3  \\ -5 \end{bmatrix} =\begin{bmatrix}2 \\1 \end{bmatrix}=\begin{bmatrix}c \\d \end{bmatrix} \Rightarrow c-3d=2-3=\bbox[red, 2pt]{-1}$$

解答: $$假設\cases{A:只報考數學A\\ B:只報考數學B\\ C:兩者都報考\\ A+B+C=1},依題意\cases{A=3/10\\ (A+C)\times {5\over 8}=C} \Rightarrow C={1\over 2} \Rightarrow B=1-{3\over 10}-{1\over 2}={2\over 10} \\ \Rightarrow 欲求{B\over B+C}={2/10\over 1/2+2/10} = \bbox[red, 2pt]{2\over 7}$$

解答: $$\overrightarrow{Q_1Q_2} =\overrightarrow{Q_1P_1} +\overrightarrow{P_1Q_2} =-\overrightarrow{P_1Q_1} + (\overrightarrow{P_1R} +\overrightarrow{RQ_2}) =-\overrightarrow{P_1Q_1} + (4\overrightarrow{P_1 Q_1 } +\overrightarrow{R P_2}+  \overrightarrow{P_2Q_2}) \\=3\overrightarrow{P_1 Q_1} -7\overrightarrow{ P_2 Q_2}+ \overrightarrow{P_2Q_2} =\bbox[red, 2pt] 3 \overrightarrow{P_1 Q_1} \bbox[red, 2pt]{-6} \overrightarrow{ P_2 Q_2}$$

解答: $$球坐標\cases{x=\rho \sin \phi \cos \theta\\ y=\rho \sin \phi \sin \theta\\ z=\rho \cos \phi \\ 北極(0,0,2) \Rightarrow \rho =2} \Rightarrow A({\sqrt 3\over 2}, {1\over 2},\sqrt 3)=(2\sin 30^\circ \cos 30^\circ,2\sin 30^\circ \sin 30^\circ, 2\cos 30^\circ)  \\ \Rightarrow \phi= 30^\circ \Rightarrow P點的\phi=90^ \circ+30^\circ =120^\circ ={2\pi\over 3} \Rightarrow 劣弧長=2\times {2\pi\over 3}=\bbox[red, 2pt]{4\pi\over 3}$$

解答:

$$假設三角形三內角分別為a,a+d,a+2d \Rightarrow 內角和=3a+3d=180 \Rightarrow a+d=60\\ \Rightarrow 三角形中間的內角為60^\circ,而正12邊形任畫三角形,最小的內角為15^\circ,\\因此有四種三角形符合條件,分別是\\\cases{ 15^\circ-60^\circ-105^\circ: 24個\\ 30^\circ-60^\circ-90^\circ: 24個\\45^\circ-60^\circ-75^\circ: 24個\\ 60^\circ-60^\circ-60^\circ:4個} \Rightarrow 共有\bbox[red, 2pt]{76}個$$

第貳部分、混 合題或非選擇題（占 15 分 ）

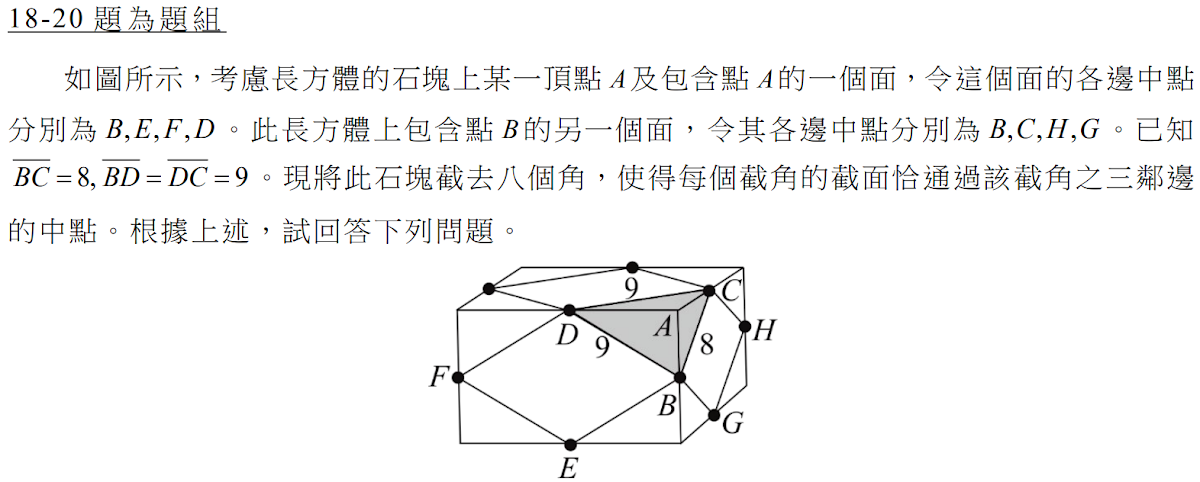
解答: $$截去八個角增加八個面,因此共有8+6=14個面, 故選\bbox[red, 2pt]{(4)}$$

解答: $$\triangle BCD三邊長為9-9-8, 為一等腰三角形, 底邊上的高=\sqrt{9^2-4^2} = \sqrt{65}\\ \Rightarrow 面積={1\over 2}\times 8\times \sqrt{65}=\bbox[red, 2pt]{4\sqrt{65}}$$

解答: $$假設\cases{\overline{AD}=a \\ \overline{AB}=b\\ \overline{AC}=c} \Rightarrow \cases{a^2+b^2=9^2\\ b^2+c^2=8^2\\ a^2+c^2= 9^2} \Rightarrow \cases{a^2=49\\b^2=32\\ c^2=32} \Rightarrow \overline{AD}=a=\bbox[red, 2pt]7 \\ 假設\cases{A(0,0,0)\\ B(4\sqrt 2,0,0)\\ C(0,4\sqrt 2,0)\\ D(0,0,7)} \Rightarrow \triangle BCD= 平面E:x+y+{4\sqrt 2\over 7}z=4\sqrt 2\\ \Rightarrow d(A,E)=高={28\sqrt 2\over \sqrt{130}} =\bbox[red, 2pt]{{28 \sqrt{65} \over 65}} \Rightarrow 體積={1\over3}\times 4\sqrt{65}\times {28\sqrt {65}\over 65} =\bbox[red, 2pt]{112\over 3}$$
 

=========================== END ==============================

解題僅供參考, 其他歷年試題及詳解