國立中山大學112學年度碩士班暨碩士在職專班招生考試試題
科目名稱:機率【通訊所碩士班甲組】
一、單選題
解答:$$兩次都得A的人數=x \Rightarrow 17+14-x+11=33 \Rightarrow x=9 \Rightarrow {9\over 33}={3\over 11},故選\bbox[red, 2pt]{(C)}$$解答:$$第八次的結果與前七次都不相同,因此機率為({5\over 6})^7, 故選\bbox[red, 2pt]{(D)}\\註: \href{https://math.stackexchange.com/questions/2946763/probability-kth-outcome-is-not-a-repetition}{參考資料}$$
解答:$$P(A\cap B) =P(A)=P(A)P(B) \Rightarrow P(A)(1-P(B))=0 \Rightarrow \cases{P(A)=0\\ P(B)=1} \\ 也就是P(A)=0或P(B)=1,故選\bbox[red, 2pt]{(E)}$$
解答:$$(D) \sum p(x) ={1\over n(n+1)}\left( 1+ 2+ \cdots +n\right) ={1\over n(n+1)}\cdot {n(n+1) \over 2}={1\over 2}\ne 1,故選\bbox[red, 2pt]{(D)}$$
解答:$$F(t)=P(X\le t)=1-P(X\gt t)=1-{1\over 2}e^{-\lambda t}-{1\over 2}e^{-\mu t} \\ \Rightarrow f(X=t) ={d\over dt}F(t)={1\over 2}\lambda e^{-\lambda t}+ {1\over 2}\mu e^{-\mu t} \Rightarrow E(X) =\int_0^\infty t\left({1\over 2}\lambda e^{-\lambda t}+ {1\over 2}\mu e^{-\mu t} \right) \,dt \\=\left.\left[{1\over 2}\lambda\left( -{e^{-\lambda t}(\lambda t+1)\over \lambda^2}\right) +{1\over 2}\mu \left( -{ e^{-\mu t}(\mu t+1)\over \mu^2}\right)\right] \right|_0^\infty ={1\over 2}\left({1\over \lambda}+{1\over \mu} \right), 故選\bbox[red, 2pt]{(B)}$$
解答:$$X\sim N(0,1) \Rightarrow pdf:f(x)={1\over \sqrt{2\pi}}e^{-x^2/2} \rightarrow f 為偶函數\\
(A)\times:g(x)=x\cos x \Rightarrow g(-x)=-g(x) \Rightarrow g為奇函數 \Rightarrow g\cdot f為奇函數 \Rightarrow E[g(x)]=0 \\(B)\times: g(x)=\sin x \Rightarrow g為奇函數 \Rightarrow g\cdot f為奇函數 \Rightarrow E[g(x)]=0 \\(C)\bigcirc: E[e^x] =\int_{-\infty}^\infty e^x\cdot {1\over \sqrt{2\pi}}e^{-x^2/2} \,dx = { \sqrt e}\int_{-\infty}^\infty {1\over \sqrt{2\pi}}e^{-(x-1)^2/2} \,dx =\sqrt e\\(D)\times: g(x)={x\over 1+x^2}\Rightarrow g為奇函數 \Rightarrow g\cdot f為奇函數 \Rightarrow E[g(x)]=0\\ 故選\bbox[red, 2pt]{(C)}$$
解答:$$(A)\bigcirc: P(Y\le y)=P(-\ln(1-X) \le y) \Rightarrow P(\ln(1-X)\ge -y) = P(X\le 1-e^{-y}) \\\qquad 若y\ge 0 \Rightarrow 1-e^{-y}\ge 0 \Rightarrow P(X\le 1-e^{-y}) = \int_0^{1-e^{-y}} 1\,dx =1-e^{-y} \\(B)\bigcirc: 若y\le 0 \Rightarrow 1-e^{-y}\le 0 \Rightarrow P(X\le 1-e^{-y}\le 0)=0 \\(C)\bigcirc: P(Z\le z)=P(X^n\le z) = P(X\le \sqrt[n] z) =\int_0^\sqrt[n]z 1\,dx=\sqrt[n] z \\(D)\times:P(X\le \sqrt[n] z) =\int_0^\sqrt[n]z 1\,dx=\sqrt[n] z\\故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{X\sim exp(1)\\ Y\sim exp(1)} \Rightarrow \cases{f_X(x)=e^{-x}, x \ge0\\ f_Y(y)=e^{-y},y\ge 0} \\ Z= \max(X,Y) \Rightarrow F_Z(z)= P(Z\le z)=P(\max(X,Y) \le z) =P(X\le z 且Y\le z) \\=P(X\le z)P(Y\le z) = \left(\int_0^z e^{-x}\,dx \right) \left( \int_0^z e^{-y} \,dy\right) =1-2e^{-z}+ e^{-2z} \\ \Rightarrow f_Z(z) ={d\over dz} (1-2e^{-z}+ e^{-2z} )=2e^{-z}-2e^{-2z} \\ \Rightarrow E[\max(X,Y)] =E[Z]= \int_0^\infty z(2e^{-z}-2e^{-2z})\,dz =2-{1\over 2}={3\over 2},故選\bbox[red, 2pt]{(B)}$$
解答:$$M_X(t)={e^t+e^{-t}\over 6}+{2\over 3} \Rightarrow \left. \frac{\text{d} }{\text{d}t}M_X(t) \right|_{t=0}= 0 \Rightarrow \left. \frac{\text{d}^2 }{\text{d}t^2}M_X(t) \right|_{t=0}= {1\over 3}\\ \Rightarrow E[X^n]=\left. \frac{\text{d}^n }{\text{d}t^n}M_X(t) \right|_{t=0}= \begin{cases}0,& n\text{ is odd} \\1/3,& n \text{ is even}\end{cases} \Rightarrow \cases{(A) \bigcirc: E[X^{1002}]=1/3\\ (B) \times:E[X^{997}]=0\\ (C)\times: E[X^{1008}]=1/3\\ (D) \times:E[X^{1008}]=1/3\\ }\\ 故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x,y)=2e^{-(x+y)},0\lt x\lt y\lt \infty \Rightarrow \cases{f_X(x)=\int_x^\infty 2e^{-(x+y)} \,dy =2e^{-2x} \\ f_Y(y)=\int_0^y2e^{-(x+y)}\,dx =2-2e^{-2y}} \\ (B)\bigcirc: f_X(x)f_Y(y)=4e^{-2x}-4e^{-2(x+y)} \ne f(x,y) \Rightarrow \text{ dependent}\\ 故選\bbox[red, 2pt]{(B)}$$
二、問答計算題
解答:$$A \text{ and }B \text{ are independent } \Rightarrow P(A\cap B) = P(A)P(B)\\ P(A\cap \bar B)=P(A)-P(A\cap B)= P(A)-P(A)P(B)=P(A)(1-P(B))=P(A)P(\bar B) \\ \Rightarrow P(A\cap \bar B)= P(A) P(\bar B) \Rightarrow A,\bar B \text{ are independent}\bbox[red, 2pt]{ Q.E.D.}$$解答:$$X\sim N(0,1) \Rightarrow f(x)={1\over \sqrt{2\pi}} e^{-x^2/2}\\ F_Y(y) =P(Y\le y) = P(e^X\le y)= P(X\le \ln y) = \int_{-\infty}^{\ln y}{1\over \sqrt{2\pi}} e^{-x^2/2} \,dx \\ \Rightarrow \text{ pdf of }Y:f_Y(y)=\frac{\text{d} }{\text{d}y} F_Y(y) = \bbox[red, 2pt]{{1\over y\sqrt{2\pi}} e^{-(\ln y)^2/2}}$$
解答:$$\textbf{(a)}\;\cases{X\sim N(0,1)\\ Y\sim N(0,1)} \Rightarrow Z=X/Y \sim \text{ Cauchy distribution } \Rightarrow \text{ pdf of }Z:\bbox[red, 2pt]{f_Z(z)={1\over \pi(z^2+1)}}\\\href{https://www.quora.com/If-X-N-0-1-and-Y-N-0-1-are-iid-random-variables-what-is-P-X-Y-t}{證明過程} \\\textbf{(b)}\; \cases{X\sim N(0,1)\\ Y\sim N(0,1)} \Rightarrow \cases{E(X+Y)=0\\ E(X-Y)=0} \\\Rightarrow COV(X+Y,X-Y) =E((X+Y)(X-Y))-E(X+Y)E(X-Y)\\ =E(X^2-Y^2)-0\cdot 0 =E(X^2)-E(Y^2)=1-1=0 \Rightarrow X+Y\text{ and }X-Y \text{ are independent }\\\qquad \bbox[red, 2pt]{Q.E.D.}$$
解答:$$\textbf{(a)}\;X=-Y \Rightarrow Z=X+Y=0 \Rightarrow f_Z(z)=\bbox[red, 2pt]0\\ \textbf{(b)}\; X=Y \Rightarrow Z=X+Y= 2X \Rightarrow F_Z(z)= P(Z\le z)=P(2X\le z)= P(x\le z/2)\\ \quad = \int_{-\infty}^{z/2} {1\over \sqrt{2\pi}} e^{-x^2/2}\,dx \Rightarrow f_Z(z)={d\over dz}\int_{-\infty}^{z/2} {1\over \sqrt{2\pi}} e^{-x^2/2}\,dx = \bbox[red, 2pt]{{1\over 2\sqrt{2\pi}} e^{-z^2/8}}$$
======================== END =====================
解題僅供參考,其他歷年試題及詳解



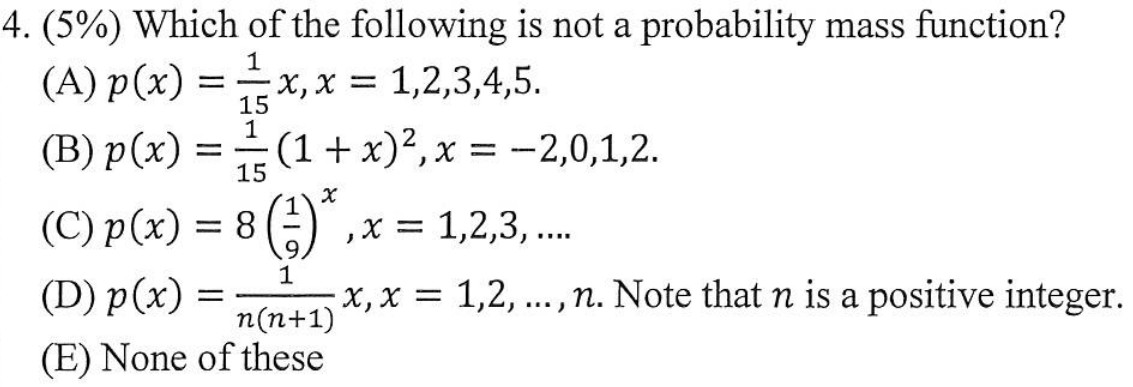








沒有留言:
張貼留言