臺北市立高級職業學校暨進修學校106 學年度聯合招考轉學生招生考試
升高二數學科試題
升高二數學科試題
$$利用餘弦定理:\vec a \cdot \vec b=|\vec a||\vec b|\cos \theta \\\Rightarrow (6,4)\cdot (5,-1)= \sqrt{6^2+4^2}\times \sqrt{5^2+1^2}\times \cos \theta\Rightarrow 26=\sqrt{52}\times \sqrt{26}\times \cos\theta\\ \Rightarrow \cos \theta = {26\over \sqrt{52\times 26}}= {1\over \sqrt{2}} \Rightarrow \theta =45^\circ, 故選:\bbox[red,2pt]{(B)}$$
解:$$f(x)=(x-4)^{2017}+3 \Rightarrow f(3)=(-1)^{2017}+3=2, 故選\bbox[red,2pt]{(C)}$$
解:
$$\begin{cases}A(2k,1)\\ B(-1,3) \\ C(-k,5)\end{cases}\Rightarrow \begin{cases} \overrightarrow{AB}=(-1-2k,2) \\ \overrightarrow{BC}= (-k+1,2)\end{cases} ;\\三點共線 \Rightarrow \overrightarrow{AB}=m \overrightarrow{BC},m為常數 \Rightarrow (-1-2k,2)=m(-k+1,2) \Rightarrow \begin{cases} -1-2k=m(-k+1) \\ 2=2m\end{cases}\\ \Rightarrow m=1 \Rightarrow -1-2k=-k+1 \Rightarrow k=-2, 故選\bbox[red,2pt]{(B)}$$
解:$$f(x)=x^2+kx-1 \Rightarrow f'(x)=2x+k \Rightarrow f'(x)=0 \Rightarrow 2x+k=0 \Rightarrow x=-k/2有極值 \\\Rightarrow -k/2=-3 \Rightarrow k=6, 故選\bbox[red,2pt]{(D)}$$
解:$$10^\circ \Rightarrow 對邊長度小於底邊\Rightarrow \cot 10^\circ > 1,其它\tan 10^\circ, \cos 10^\circ及\sin 10^\circ均小於1, 故選\bbox[red,2pt]{(A)}$$
解:
$$P=\left( {1\times 1+3\times(-7) \over 4}, {1\times (-12)+3\times 4 \over 4}\right) =(-5,0), 故選\bbox[red,2pt]{(D)}$$
解:
$$x={-1+\sqrt 5\over 2} \Rightarrow 2x+1=\sqrt 5 \Rightarrow (2x+1)^2=5 \Rightarrow 4x^2+4x-4=0 \Rightarrow x^2+x=1 \\ \Rightarrow x^3+3x^2+x+3 = x(x^2+x)+x^2+(x^2+x)+3 =x+x^2+4=1+4=5, 故選\bbox[red,2pt]{(C)}$$
解:$$L的斜率為-{2\over 5} \Rightarrow L: y=-{2\over 5}x+b,又經過(3,2) \Rightarrow 2= -{6\over 5}+b \Rightarrow b= {16\over 5} \Rightarrow L:y=-{2\over 5}x+{16 \over 5}\\ \Rightarrow \begin{cases}L與x軸交於A(8,0)\\ L與y軸交於B(0,{16\over 5}) \end{cases} \Rightarrow \triangle OAB= \overline{OA}\times \overline{OB}\div 2=8\times {16\over 5}\times {1\over 2}= {64\over 5},故選\bbox[red,2pt]{(A)} $$
解:$$|3\vec a-2\vec b|^2=(3\vec a-2\vec b)\cdot (3\vec a-2\vec b) = 9|\vec a|^2-12(\vec a\cdot \vec b) + 4|\vec b|^2 =36-36+36=36 \\ \Rightarrow |3\vec a-2\vec b|=\sqrt {36}=6,故選\bbox[red,2pt]{(B)} $$
解:$$(a+b):(b+c):(c+a) =5:4:6 \Rightarrow \begin{cases}a+b=5k\cdots (1)\\ b+c=4k\cdots (2) \\ c+a=6k\cdots (3) \end{cases} \Rightarrow (1)+(2)+(3) \Rightarrow 2(a+b+c)=15k\\ \Rightarrow a+b+c={15\over 2}k\cdots(4);因此 \begin{cases}(4)-(1) \Rightarrow c=5k/2\\ (4)-(2) \Rightarrow a=7k/2 \\ (4)-(3) \Rightarrow b=3k/2 \end{cases} \Rightarrow a:b:c=7:3:5 \\ 由正弦定理: {a\over \sin A} ={b\over \sin B} ={c\over \sin C} \Rightarrow \sin A:\sin B:\sin C=a:b:c = 7:3:5 ,故選\bbox[red,2pt]{(C)}$$
解:$$令直線\overline{AB}的方程式為: y=ax+b,由\begin{cases}A(1-3)\\ B(7,5) \end{cases} \Rightarrow \begin{cases}-3=a+b\\ 5=7a+b \end{cases} \Rightarrow \begin{cases}a=4/3\\ b=-13/3 \end{cases} \Rightarrow y={4\over 3}x-{13\over 3} \\ \Rightarrow 4x-3y-13=0 \Rightarrow C至\overline{AB}的距離=\left| \cfrac{-8-9-13}{\sqrt{4^2+3^2}}\right|=\frac{30}{5} =6,故選\bbox[red,2pt]{(C)}$$
解:$$\alpha,\beta 為x^2+2x-5=0的兩根 \Rightarrow \begin{cases}\alpha+\beta=-2\\ \alpha\beta=-5 \end{cases} \Rightarrow (\alpha+\beta)^2= \alpha^2+\beta^2 +2\alpha\beta \\\Rightarrow (-2)^2=\alpha^2+\beta^2+2(-5) \Rightarrow \alpha^2+\beta^2=4+10=14,故選\bbox[red,2pt]{(A)}$$
解:$$f(x)=-x^2+4x-1 =-(x^2-4x+4)+3 =-(x-2)^2+3 \Rightarrow 圖形為凹向下,頂點位於(2,3),\\又f(0)=-1 \Rightarrow 該圖形不經過第二象限,故選\bbox[red,2pt]{(B)}$$
解:
$$\begin{cases} (A):-4\pi/3 =2\pi-4\pi/3= 2\pi/3 =120^\circ\\ (B):480^\circ =480^\circ-360^\circ =120^\circ \\ (C):-2\pi/3 = 2\pi-2\pi/3=4\pi/3=240^\circ\\ (D):3000^\circ =360^\circ\times 8+120^\circ= 120^\circ\end{cases} ,故選\bbox[red,2pt]{(C)}$$
解:$$\begin{cases} \vec a=(2,1)\\\vec b=(5,2)\\ \vec c=(12,5)\end{cases} \Rightarrow \vec c=\alpha \vec a+\beta \vec b \Rightarrow (12,5)=\alpha(2,1)+\beta (5,2) \Rightarrow \begin{cases} 2\alpha +5\beta=12\\ \alpha+2\beta=5 \end{cases} \Rightarrow \begin{cases} \alpha=1\\ \beta=2 \end{cases} \\ \Rightarrow \alpha+\beta=1+2=3\\,故選\bbox[red,2pt]{(D)}$$
解:$$(A)\bigcirc: |x-1|=0 \Rightarrow x=1\\(B)\times:|x-1|=2 \Rightarrow x=3,-1\\(C) -2x^2+4x+6=0 \Rightarrow x^2-2x-3=0 \Rightarrow (x-3)(x+1)=0 \Rightarrow x=3,-1\\(D)-2x^2+4x-6 \Rightarrow 判別式 4^2-4\times(-1)(-6) =16-24<0 \Rightarrow 無實數解\\,故選\bbox[red,2pt]{(A)} $$
解:$$x>y>0 \Rightarrow \begin{cases}\sqrt{(y-x)^2} =x-y \\\sqrt[3]{(y-x)^3} =y-x\end{cases} \Rightarrow \sqrt{(y-x)^2}-\sqrt[3]{(y-x)^3}=x-y-(y-x)=2x-2y\\,故選\bbox[red,2pt]{(A)}$$
解:$$\begin{vmatrix}
a & d & g\\
b & e & h\\
c & f & i
\end{vmatrix} =-3 \Rightarrow \begin{vmatrix}
a & g & d\\
b & h & e\\
c & i &f
\end{vmatrix} =3 \Rightarrow \begin{vmatrix}
a+3g & g & d\\
b+3h & h & e\\
c+3i & i &f
\end{vmatrix} =3 \\\Rightarrow \begin{vmatrix}
a+3g & -2g & d\\
b+3h & -2h & e\\
c+3i & -2i &f
\end{vmatrix} =3\times (-2)=-6,故選\bbox[red,2pt]{(B)}$$
解:$$\begin{cases}x+ky=5 \\ kx+4y= 10\end{cases} 無解\Rightarrow {1\over k} ={k\over 4}\ne {5\over 10} \Rightarrow \begin{cases}k^2=4 \\ k\ne 2\end{cases} \Rightarrow k=-2,故選\bbox[red,2pt]{(A)}$$
解:
$$由上圖可知,交接區域不含第二象限,故選\bbox[red,2pt]{(B)}$$
解:$$令f(x,y)=3x+4y,則\begin{cases}x\ge 0\\ y\ge 0\\ 2x+y\ge 4\\ 3x+2y\ge 6\end{cases} 形成封半閉區域的頂點為 \begin{cases}A(0,4)\\ B(2,0)\end{cases} \Rightarrow \begin{cases}f(A)=14\\ f(B)=6\end{cases}\\ \Rightarrow 3x+4y的最小值為6,最大值為\infty,故選\bbox[red,2pt]{(C)}$$
解:$$x-x^2+6 \le 0 \Rightarrow x^2-x-6 \ge 0 \Rightarrow (x-3)(x+2) \ge 0 \Rightarrow x\ge 3 或x\le -2,故選\bbox[red,2pt]{(D)}$$
解:
$$(x^2+(2y)^2)(3^2+(-1)^2) \ge (3x-2y)^2 \Rightarrow 10\times 10 \ge (3x-2y)^2 \Rightarrow 10 \ge 3x-2y\\ \Rightarrow 3x-2y 的最大值為10,故選\bbox[red,2pt]{(D)}$$
解題僅供參考















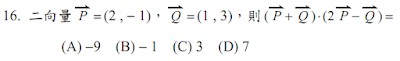










沒有留言:
張貼留言