111 學年度科技校院四年制與專科學校二年制
統一入學測驗-數學(A)
解答:
$$\cases{x+y\le 2,藍色區域\\ 3x+y\ge 3,紅色區域} \Rightarrow 兩著色區域交集即為所求,故選\bbox[red, 2pt]{(D)}$$
解答:$$a={1\over 2} \Rightarrow \cases{a^2 = 1/4\\ a^{-2}=4} \Rightarrow a^2+2+a^{-2}= {1\over 4}+2+ 4={25\over 4};\\ 也可以利用a^2+2+a^{-2}=(a+{1\over a})^2 =({1\over 2}+2)^2 = ({5\over 2})^2 ={25\over 4},故選\bbox[red, 2pt]{(D)}$$
解答:$$(A)\times: \cases{a\times b= \log 5\times \log 2\\ \log 5+\log 2= \log 10=1} \Rightarrow a\times b\ne \log 5+\log 2\\ (B)\times: a\div b= \log 5\div \log 2 \ne {5\over 2}\\ (C)\bigcirc: a+b=\log 5+ \log 2=\log 10=1\\ (D)\times: a-b =\log 5-\log 2=\log {5\over 2} \ne {\log 5\over \log 2}\\,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x,y)=(x-y)^3 = x^3-3x^2y+3xy^2-y^3 \Rightarrow f({7\over 8},{3\over 8})=({7\over 8}-{3\over 8})^3=({1\over 2})^3 ={1\over 8},故選\bbox[red, 2pt]{(A)}$$
解答:$$每週藥量成等差數列,即\cases{a_1= 2\times 7=14\\ d=-3.5\\ a_n=0.5\times 7=3.5} \Rightarrow a_n = a_1+(n-1)d \Rightarrow 3.5= 14-3.5(n-1)\\ \Rightarrow n-1={14-3.5\over 3.5} ={10.5\over 3.5}=3 \Rightarrow n=4,故選\bbox[red, 2pt]{(B)}$$
解答:$$f(x,y)=3x+4y+5 \Rightarrow \cases{f(1,1)=12 \gt 0\\ (A): f(-1,-1)=-2\lt 0\\ (B):f(1,-3)=-4\lt 0\\ (C):f(-1,-2)=-6\lt 0\\ (D): f(-2,1)=-6+4+5=1\gt 0} \\\Rightarrow f(1,1)與f(-2,1)同號,故選\bbox[red, 2pt]{(D)}$$
解答:$$全距=最大值-最小值,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=(x+3)^2-12 \Rightarrow (m,n)=(-3,-12) \Rightarrow 2m-n=-6+12= 6,故選\bbox[red, 2pt]{(A)}$$
解答:$$假設中午溫度為攝氏a度 \Rightarrow 夜間為攝氏a-9度,相當於\cases{中午華氏({9\over 5}a+32)度\\[1ex] 夜間華氏({9\over 5}(a-9)+32)度} \\ \Rightarrow 華氏溫差({9\over 5}a+32)-({9\over 5}(a-9)+32) ={9\over 5}\times 9={81\over 5} \approx 16,故選\bbox[red, 2pt]{(B)}$$
解答:$$\angle CAB=\angle TAS \Rightarrow \triangle AST \sim \triangle ABC(AAA) \Rightarrow \overline{TS}:\overline{SA} =\overline{CB}: \overline{AB} \Rightarrow 120:250= \overline{CB}:450\\ \Rightarrow \overline{BC}={120\times 450\over 250} = 216,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=(x-2)(x-3)(2x-3)(x-1)+2x+3 = (x-1)(x-3)p(x)+ax+b\\ \Rightarrow \cases{f(1)=2+3=5=a+b \\f(3)=6+3=9=3a+b} \Rightarrow \cases{a=2\\ b=3} \Rightarrow a-b=2-3=-1,故選\bbox[red, 2pt]{(A)}$$
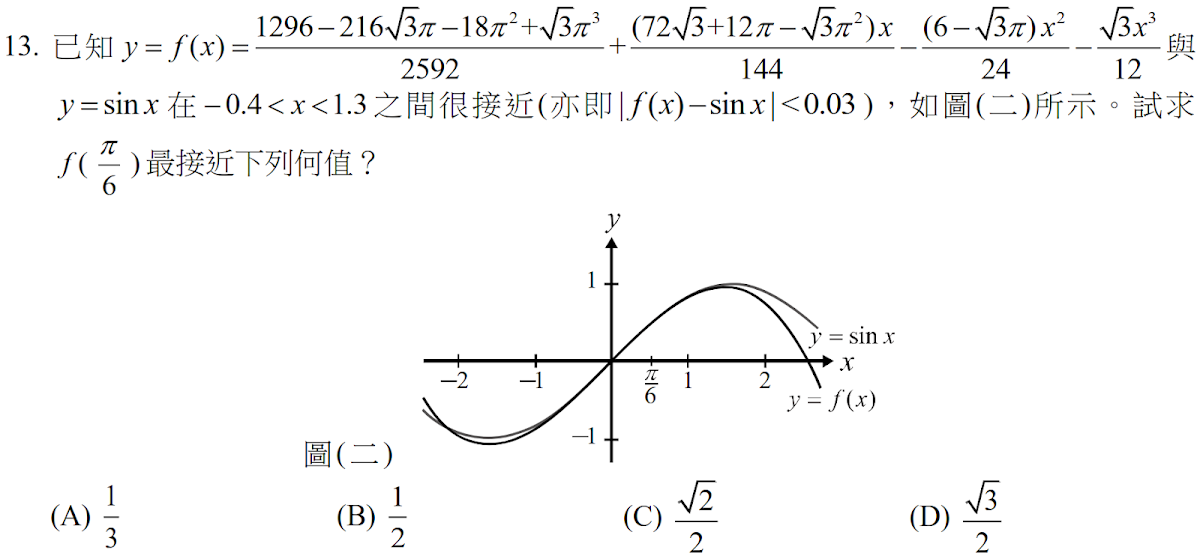
解答:$$-0.4\lt {\pi \over 6}\lt 1.3 \Rightarrow f({\pi \over 6}) \approx \sin {\pi \over 6} = {1\over 2},故選\bbox[red, 2pt]{(B)}$$
解答:$$甲、乙、丙三人皆有4種選擇,僅有丙只有3種選擇,故共有4^3\times 3=192種方法數,故選\bbox[red, 2pt]{(C)}$$
解答:$$先抽班級再抽個人,班級是抽樣,但個人的部份是普查,故選\bbox[red, 2pt]{(D)}$$
解答:$$C^4_2\times C^4_2= 36,故選\bbox[red, 2pt]{(C)}$$
解答:$$3.5\times 80+5=285,故選\bbox[red, 2pt]{(C)}$$
解答:$$面積成等差,即3^2,r^2,1^2成等差,r^2=(9+1)\div 2=5,中圓半徑r=\sqrt 5 \\\Rightarrow 中圓方程式: (x-1)^2+(y+1)^2 =5,故選\bbox[red, 2pt]{(B)}$$
解答:$$每經一次裁剪後,面積少了{1\over 9},剩下1-{1\over 9}= {8\over 9},因此經過6次裁剪後,剩下({8\over 9})^6,故選\bbox[red, 2pt]{(C)}$$
解答:$$(A)\times: \cases{a\times b= \log 5\times \log 2\\ \log 5+\log 2= \log 10=1} \Rightarrow a\times b\ne \log 5+\log 2\\ (B)\times: a\div b= \log 5\div \log 2 \ne {5\over 2}\\ (C)\bigcirc: a+b=\log 5+ \log 2=\log 10=1\\ (D)\times: a-b =\log 5-\log 2=\log {5\over 2} \ne {\log 5\over \log 2}\\,故選\bbox[red, 2pt]{(C)}$$
解答:$$f(x,y)=(x-y)^3 = x^3-3x^2y+3xy^2-y^3 \Rightarrow f({7\over 8},{3\over 8})=({7\over 8}-{3\over 8})^3=({1\over 2})^3 ={1\over 8},故選\bbox[red, 2pt]{(A)}$$
解答:$$每週藥量成等差數列,即\cases{a_1= 2\times 7=14\\ d=-3.5\\ a_n=0.5\times 7=3.5} \Rightarrow a_n = a_1+(n-1)d \Rightarrow 3.5= 14-3.5(n-1)\\ \Rightarrow n-1={14-3.5\over 3.5} ={10.5\over 3.5}=3 \Rightarrow n=4,故選\bbox[red, 2pt]{(B)}$$
解答:$$f(x,y)=3x+4y+5 \Rightarrow \cases{f(1,1)=12 \gt 0\\ (A): f(-1,-1)=-2\lt 0\\ (B):f(1,-3)=-4\lt 0\\ (C):f(-1,-2)=-6\lt 0\\ (D): f(-2,1)=-6+4+5=1\gt 0} \\\Rightarrow f(1,1)與f(-2,1)同號,故選\bbox[red, 2pt]{(D)}$$
解答:$$全距=最大值-最小值,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=(x+3)^2-12 \Rightarrow (m,n)=(-3,-12) \Rightarrow 2m-n=-6+12= 6,故選\bbox[red, 2pt]{(A)}$$
解答:$$假設中午溫度為攝氏a度 \Rightarrow 夜間為攝氏a-9度,相當於\cases{中午華氏({9\over 5}a+32)度\\[1ex] 夜間華氏({9\over 5}(a-9)+32)度} \\ \Rightarrow 華氏溫差({9\over 5}a+32)-({9\over 5}(a-9)+32) ={9\over 5}\times 9={81\over 5} \approx 16,故選\bbox[red, 2pt]{(B)}$$
解答:$$\angle CAB=\angle TAS \Rightarrow \triangle AST \sim \triangle ABC(AAA) \Rightarrow \overline{TS}:\overline{SA} =\overline{CB}: \overline{AB} \Rightarrow 120:250= \overline{CB}:450\\ \Rightarrow \overline{BC}={120\times 450\over 250} = 216,故選\bbox[red, 2pt]{(A)}$$
解答:$$f(x)=(x-2)(x-3)(2x-3)(x-1)+2x+3 = (x-1)(x-3)p(x)+ax+b\\ \Rightarrow \cases{f(1)=2+3=5=a+b \\f(3)=6+3=9=3a+b} \Rightarrow \cases{a=2\\ b=3} \Rightarrow a-b=2-3=-1,故選\bbox[red, 2pt]{(A)}$$
解答:$$-0.4\lt {\pi \over 6}\lt 1.3 \Rightarrow f({\pi \over 6}) \approx \sin {\pi \over 6} = {1\over 2},故選\bbox[red, 2pt]{(B)}$$
解答:$$甲、乙、丙三人皆有4種選擇,僅有丙只有3種選擇,故共有4^3\times 3=192種方法數,故選\bbox[red, 2pt]{(C)}$$
解答:$$先抽班級再抽個人,班級是抽樣,但個人的部份是普查,故選\bbox[red, 2pt]{(D)}$$
解答:$$C^4_2\times C^4_2= 36,故選\bbox[red, 2pt]{(C)}$$
解答:$$3.5\times 80+5=285,故選\bbox[red, 2pt]{(C)}$$
解答:$$面積成等差,即3^2,r^2,1^2成等差,r^2=(9+1)\div 2=5,中圓半徑r=\sqrt 5 \\\Rightarrow 中圓方程式: (x-1)^2+(y+1)^2 =5,故選\bbox[red, 2pt]{(B)}$$
解答:$$每經一次裁剪後,面積少了{1\over 9},剩下1-{1\over 9}= {8\over 9},因此經過6次裁剪後,剩下({8\over 9})^6,故選\bbox[red, 2pt]{(C)}$$
解答:$$\overline{AD}: \overline{DB}=1:2 \Rightarrow D=(B+2A)\div 3=({2+2\cdot 8\over 3},{1+2\cdot 7\over 3})=(6,5)\\\overleftrightarrow{AC}斜率m={3-7\over 12-8}=-1 \Rightarrow 通過D(6,5)且斜率為-1的直線方程式:y=-(x-6)+5 \\\Rightarrow x+y-11=0,故選\bbox[red, 2pt]{(D)}$$
解答:$$假設承攬\cases{10萬預算案x件\\20萬預算y件 \\30萬預算案z件},符合x+y+z=5,且\cases{1\le x\le 4\\ 1\le y\le 3\\ 1\le z\le 2} \\ \Rightarrow a+b+c=2,其中\cases{a=x-1\\ b=y-1\\ c=z-1},並符合\cases{0\le a\le 3\\ 0\le b\le 2\\ 0\le c\le 1},\\滿足以上條件的(a,b,c)整數解共有H^3_2 = C^4_2=6種,但需扣除(a,b,c)=(0,0,2)(因為c\le 1),\\因此共有6-1=5種方法,故選\bbox[red, 2pt]{(B)}$$
解答:
解答:$$假設承攬\cases{10萬預算案x件\\20萬預算y件 \\30萬預算案z件},符合x+y+z=5,且\cases{1\le x\le 4\\ 1\le y\le 3\\ 1\le z\le 2} \\ \Rightarrow a+b+c=2,其中\cases{a=x-1\\ b=y-1\\ c=z-1},並符合\cases{0\le a\le 3\\ 0\le b\le 2\\ 0\le c\le 1},\\滿足以上條件的(a,b,c)整數解共有H^3_2 = C^4_2=6種,但需扣除(a,b,c)=(0,0,2)(因為c\le 1),\\因此共有6-1=5種方法,故選\bbox[red, 2pt]{(B)}$$
解答:
$$假設A為原點,各點坐標如上圖所示,其中D(12,6)為基地台,則直線L=\overleftrightarrow{AB}:4x=3y;\\ 因此\cases{\overline{AD}=\sqrt{12^2+6^2}=\sqrt {180} \gt 9 \\\overline{BD}= 10\gt 9\\ d(D,L)={48-18\over \sqrt{3^2+4^2}}= 6\lt 9} \\\Rightarrow 在線段\overline{AB}中間有一段在服務範圍內,其它不屬於服務範圍,故選\bbox[red, 2pt]{(A)}$$
解答:$$六球取三球有C^6_3=20種取法;而最小編號為9的取法:(9,10,11),(9,10,12),(9,11,12)三種取法\\,因此機率為{3\over 20},故選\bbox[red, 2pt]{(A)}$$
解答:$$\alpha,\beta 為x^2+x-1=0的兩根\Rightarrow \cases{\alpha +\beta =-1\\ \alpha\beta=-1} \\\Rightarrow \cases{({\beta\over \alpha}+1) +({\alpha\over \beta}+1)= {\alpha^2+\beta^2 \over \alpha\beta}+2 ={(\alpha +\beta)^2 -2\alpha\beta \over \alpha\beta}+2 ={(\alpha +\beta)^2 \over \alpha\beta}=-1\\ ({\beta\over \alpha}+1)({\alpha\over \beta}+1)=({\beta\over \alpha}+1) +({\alpha\over \beta}+1)=-1} \\ \Rightarrow 以({\beta\over \alpha}+1) ,({\alpha\over \beta}+1)為兩根的方程式:x^2+x-1=0,故選\bbox[red, 2pt]{(D)}$$
解答:
解答:$$六球取三球有C^6_3=20種取法;而最小編號為9的取法:(9,10,11),(9,10,12),(9,11,12)三種取法\\,因此機率為{3\over 20},故選\bbox[red, 2pt]{(A)}$$
解答:$$\alpha,\beta 為x^2+x-1=0的兩根\Rightarrow \cases{\alpha +\beta =-1\\ \alpha\beta=-1} \\\Rightarrow \cases{({\beta\over \alpha}+1) +({\alpha\over \beta}+1)= {\alpha^2+\beta^2 \over \alpha\beta}+2 ={(\alpha +\beta)^2 -2\alpha\beta \over \alpha\beta}+2 ={(\alpha +\beta)^2 \over \alpha\beta}=-1\\ ({\beta\over \alpha}+1)({\alpha\over \beta}+1)=({\beta\over \alpha}+1) +({\alpha\over \beta}+1)=-1} \\ \Rightarrow 以({\beta\over \alpha}+1) ,({\alpha\over \beta}+1)為兩根的方程式:x^2+x-1=0,故選\bbox[red, 2pt]{(D)}$$
解答:
$$兩直線\cases{x+y=1\\ 3x+y=3}的交點A(1,0) \Rightarrow f(1,0)=2+0=2,故選\bbox[red, 2pt]{(B)}$$
==================== END =========================
解題僅供參考,其他歷年試題及詳解




























沒有留言:
張貼留言