113年新竹高中教甄-數學詳解

新竹中學 113 學年度教師第一次教師甄試數學科題目卷

一、填空題： 12 格，每格 6 分

解答：

$${x^2\over 3}-{y^2\over 2}=1 \Rightarrow \cases{a=\sqrt 3\\ b=\sqrt 2} \Rightarrow c=\sqrt 5 \Rightarrow \cases{F_1(\sqrt 5,0)\\ F_2(-\sqrt 5,0)} \\又 {2\over 3}x-yy'=0 \Rightarrow y'={2x\over 3y} \Rightarrow \left. y \right|_{(3,-2)}'= {6\over -6} =-1 \\ \Rightarrow 切線方程式：y+2=-(x-3) \Rightarrow x+y=1 \Rightarrow Q(1,0) \\ \Rightarrow \cases{F_1(\sqrt 5,0) \\P(3,-2)\\ Q(1,0)\\ A(3,)\\ \angle APF_1=\theta_1\\ \angle F_1PQ=\theta_2} \Rightarrow \triangle PAQ為等腰直角\triangle  \Rightarrow \cases{ \tan\theta_1=(3-\sqrt 5)/2 \\ \tan \angle APQ= \tan( \theta_1+ \theta_2)=1} \\ \Rightarrow \cfrac{\tan\theta_2+{3-\sqrt 5\over 2}}{1-\tan\theta_2\cdot {3-\sqrt 5\over 2}} =1 \Rightarrow \tan \theta_2={-1+\sqrt 5\over 5-\sqrt 5} = \bbox[red, 2pt]{\sqrt 5\over 5}$$

解答： $$a+c=2b \Rightarrow \sin A+\sin C=2\sin B \Rightarrow 2\sin{A+C\over 2} \cos{A-C\over 2}= 4\sin{B\over 2}\cos{B\over 2} \\ \Rightarrow 2\sin({\pi\over 2}-{B\over 2})\cos{A-C\over 2}= 4\sin{B\over 2}\cos{B\over 2} \Rightarrow \cos{A-C\over 2}=2\sin{B\over 2} \\ \Rightarrow \cos {\pi\over 6}={\sqrt 3\over 2} =2\sin{B\over 2} \Rightarrow \sin {B\over 2}={\sqrt 3\over 4} \Rightarrow \cos B=1-2\sin^2{B\over 2} = \bbox[red, 2pt]{{5\over 8}}$$

解答： $$\triangle OPR面積=7 \Rightarrow \overrightarrow{OP}與\overrightarrow{OR}所張出的平行四邊形面積=14\\ \overrightarrow{OB} =x\overrightarrow{OP} +y\overrightarrow{OR} \Rightarrow \cases{x= {\overrightarrow{OB}與\overrightarrow{OR}所張出的平行四邊形面積 \over \overrightarrow{OP}與\overrightarrow{OR}所張出的平行四邊形面積} ={14\over 14} =1\\y= {\overrightarrow{OB}與\overrightarrow{OP}所張出的平行四邊形面積 \over \overrightarrow{OP}與\overrightarrow{OR}所張出的平行四邊形面積} ={28\over 14} =2} \\ \Rightarrow (x,y)=\bbox[red, 2pt]{(1,2)}$$

解答： $$\cases{5=1+4=2+3=3+2 =4+1 \Rightarrow 擲出點數和為5的機率p={4\over 36} ={1\over 9} \\7= 1+6= 2+5+3+4=4+3 =5+2 =6+1 \Rightarrow 擲出點數和為7的機率q={6\over 36} ={1\over 6}}\\ \Rightarrow 不是5也不是7的機率r=1-{1\over 9}-{1\over 6}={13\over 18}\\點數和為5比點數和為7先出現的情形：\\1.只擲1次：第1次擲就出現5，機率=p\\ 2.擲2次：第1次不是5也不是7，但第2次一定是5，機率=rp\\ 3.擲3次：第1次及第2次都不是5也不是7，但第3次一定是5，機率=r^2p\\ 4.擲n次：第1次到及第n－1次都不是5也不是7，但第n次一定是5，機率=r^{n-1}p\\ 機率總和=p+pr+pr^2+\cdots+pr^{n-1}+\cdots =p{1\over 1-r}={1\over 9}\cdot {18\over 5}= \bbox[red, 2pt]{2\over 5}$$

解答：

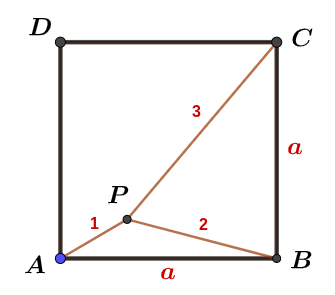
$$假設正方形邊長為a\Rightarrow \cases{\cos \angle PBA={a^2+3\over 4a} \\ \cos \angle PBC ={a^2-5\over 4a}}\\ \angle PBC+\angle PBC=90^\circ \Rightarrow \cos^2 \angle PBA+ \cos^2\angle PBC=1 \Rightarrow \left( {a^2+3\over 4a}\right)^2 +\left( {a^2-5\over 4a}\right)^2 =1 \\ \Rightarrow 2a^4-4a^2+34=16a^2 \Rightarrow a^4-10a^2+17=0 \Rightarrow 面積=a^2=\bbox[red, 2pt]{5+2\sqrt{2}}$$

解答： $$f'(x)={-3\sqrt{2x-1}+2\sqrt{4-3x} \over 2\sqrt{4-3x}\cdot \sqrt{2x-1}} =0 \Rightarrow 2\sqrt{4-3x}= 3\sqrt{2x-1} \Rightarrow x={5\over 6} \\ \Rightarrow \cases{f({5\over 6})={5\sqrt 6\over 6} \\ f({1\over 2})=\sqrt{5\over 2} \\f({4\over 3}) =\sqrt{5\over 3}} \Rightarrow f(5/6) \gt f(1/2)\gt f(4/3) \Rightarrow (\alpha,M)=\bbox[red, 2pt]{({5\over 6},{5\sqrt 6\over 6})}$$

解答： $$a^2+b^2要最大\Rightarrow y=x^2-ax+b圖形在x軸最寬 \Rightarrow x^2-ax+b=(x+1)(x-2)= x^2-x-2 \\ \qquad \Rightarrow a^2+b^2=1+4=5 \Rightarrow M=5\\ a^2+b^2要最小，先假設\beta=1 \Rightarrow x^2-ax+b =(x-\alpha)(x-1)= x^2-(\alpha+1) x+\alpha \\\qquad a^2+b^2= (\alpha+1)^2+\alpha^2 =2\alpha^2+2\alpha+1 \Rightarrow \alpha=-{1\over 2} \Rightarrow a^2+b^2={1\over 2} \\ 再假設\alpha=0 \Rightarrow x^2-ax+b=x(x-\beta) =x^2-\beta x \Rightarrow a^2+b^2=\beta^2 最小值＝1\lt {1\over 2} \\ 因此m={1\over 2} \Rightarrow (M,m)= \bbox[red, 2pt]{(5,{1\over 2})}$$

解答： $$錯誤公式：\cfrac{\sum(x_i+ \mu_x)(y_i+\mu_y)}{\sum(x_i+\mu_x)^2} =\cfrac{ \sum(x_iy_i+ \mu_x y_i+x_i\mu_y +\mu_x \mu_y)}{\sum(x_i^2+2\mu_x x_i +\mu_x^2)} \\= \cfrac{ \sum(x_iy_i+ 2 y_i+ 8x_i +16)}{\sum(x_i^2+ 4 x_i + 4)} = \cfrac{ \sum x_iy_i+ 2 \sum y_i+ 8\sum x_i +\sum16 }{\sum x_i^2+ 4 \sum x_i + \sum4} \\= \cfrac{ \sum x_iy_i+ 2 (5\cdot 8)+ 8(5\cdot 2) +16\cdot 5 }{30+ 4 (5\cdot 2) + 4 \cdot 5} = \cfrac{ \sum x_iy_i+ 240 }{90} ={10\over 3} \Rightarrow \sum x_iy_i=60 \\正確公式：\cfrac{\sum(x_i-\mu_x)(y_i-\mu_y)}{\sum(x_i-\mu_x)^2}=\cfrac{ \sum(x_iy_i- \mu_x y_i-x_i\mu_y +\mu_x \mu_y)}{\sum(x_i^2-2\mu_x x_i +\mu_x^2)} \\=\cfrac{60-80-80+80}{30-40+20}=-2 \Rightarrow 迴歸直線：y-\mu_y=-2(x-\mu_x) \Rightarrow \bbox[red, 2pt]{y-8 =-2(x-2)}$$

解答： $$\cases{A(2,3,6)\\ B(6,2,3)\\ C(3,6,2)} \xrightarrow{將原點平移至A} \cases{A(0,0,0)\\ B(4,-1,-3)\\ C(1,3,-4)} \Rightarrow \cases{平面E=\triangle ABC:x+y+z=0\\ G=\triangle ABC重心=(5/3,2/3,-7/3)}\\ 直線L通過G且方向向量=(1,1,1) \Rightarrow L:(t+{5\over 3},t+{2\over 3},t-{7\over 3}),t\in \mathbb R\\ D在L上\Rightarrow D((s+{5\over 3},s+{2\over 3},s-{7\over 3}),s\in \mathbb R \\ \cases{\overrightarrow{AB}=(4,-1,-3)\\ \overrightarrow{CD}= (s+{2\over 3}, s-{7\over 3},s+{5\over 3})} \Rightarrow \vec u= \overrightarrow{AB} \times \overrightarrow{CD} = \left(2s-{26\over 3}, -7s-{26\over 3},5s-{26\over 3}  \right) \\ \Rightarrow \overrightarrow{AC} =(1,3,-4)在 \vec u上的投影={13\over \sqrt{10}} \Rightarrow {\overrightarrow{AC} \cdot \vec u\over |\vec u|} ={-39s \over \sqrt{78s^2+{676\over 3}}} ={13 \over \sqrt{10}} \\ \Rightarrow 2028s^2= {114244\over 3} \Rightarrow \cases{s={13\over 3}\\ s=-{13\over 3}} \Rightarrow \cases{D=(6,5,2)\\ D=(-{8\over 3},-{11\over 3}, -{20\over 3})} \\\xrightarrow {平移回去} \cases{D=(6,5,2)+(2, 3,6)=(8,8,8) \\ D=(-{8\over 3},-{11\over 3}, -{20\over 3}) +(2,3,6) =(-{2\over 3},-{2\over 3} ,-{2\over 3})} \Rightarrow D=\bbox[red, 2pt]{(8,8,8),(-{2\over 3},-{2\over 3} ,-{2\over 3})}$$

解答：

$$A,B為切點 \Rightarrow \angle CAP=\angle CBP=90^\circ \Rightarrow \cases{外接圓圓心Q(6,4)為\overline{CP}的中點 \\ \overline{CP}為外接圓直徑}\\ 假設C(a,b) \Rightarrow Q=(P+C)\div 2 \Rightarrow P(12-a,8-b)\\ \Rightarrow \cases{切線L_1=\overleftrightarrow{AP}: y={2\over 3}(x-12+a)+8-b \\ 切線L_2=\overleftrightarrow{BP}: y={3\over 2}(x-12+a)+8-b}\Rightarrow \cases{L_1:2x-3y+2a-3b=0\\ L_2:3x-2y+3a-2b-20=0}\\ \Rightarrow \cases{d(C,L_1)=4\sqrt{13} \\ d(C,L_2)=4\sqrt{13}}  \Rightarrow \cases{\cfrac{|4a-6b|}{\sqrt{13}} =4\sqrt{13} \\ \cfrac{|6a-4b-20| }{\sqrt{13}} = 4\sqrt{13}} 有四種可能，挑a,b\lt 0\\ \Rightarrow \cases{4a-6b=52\\ 6a-4b-20=-52} \Rightarrow \cases{a=-20\\ b=-22} \Rightarrow C\bbox[red, 2pt]{(-20,-22)}$$

解答： $$\cases{1^\circ={\pi \over 180} \\ \sum_{k=1}^n k(k+1)(k+2)={1\over 4}n(n+1)(n+2)(n+3)\\ \sum_{k=1}^n k(k+1)(k+2)(k+3) ={1\over 5}n(n+1)(n+2)(n+3) (n+4)} \\ \Rightarrow \lim_{n\to \infty} a_n=  \lim_{n\to \infty} \sin {\pi\over 180 n} \cdot {4\over 5}(n+4)=  \lim_{n\to \infty} \cfrac{{4\over 5}\sin {\pi\over 180 n}}{ { 1\over n+4}} \\=  \lim_{n\to \infty} \cfrac{\left({4\over 5}\sin {\pi\over 180 n}\right)'}{ ({ 1\over n+4})'} =  \lim_{n\to \infty} \cfrac{{4\over 5} \cdot {-{\pi \over 180n^2}}\cos {\pi\over 180 n}}{ -{ 1\over (n+4)^2}} ={4\over 5} \cdot {\pi \over 180} = \bbox[red, 2pt]{\pi \over 225}$$

解答： $$\begin{bmatrix}\cos a^\circ & \sin a^\circ\\ \sin a^\circ & -\cos a^\circ \end{bmatrix} \begin{bmatrix}\cos (a+1)^\circ & \sin (a+1)^\circ\\ \sin (a+1)^\circ & -\cos (a+1)^\circ \end{bmatrix} =\begin{bmatrix}\cos 1^\circ & \sin 1^\circ \\-\sin 1^\circ & \cos 1^\circ \end{bmatrix} \\ \Rightarrow B=\begin{bmatrix}\cos 1^\circ & \sin 1^\circ \\-\sin 1^\circ & \cos 1^\circ \end{bmatrix}^{30}= \begin{bmatrix}\cos 2^\circ & \sin 2^\circ \\-\sin 2^\circ & \cos 2^\circ \end{bmatrix}^{15} = \begin{bmatrix}\cos 4^\circ & \sin 4^\circ \\-\sin 4^\circ & \cos 4^\circ \end{bmatrix}^{7} \begin{bmatrix}\cos 2^\circ & \sin 2^\circ \\-\sin 2^\circ & \cos 2^\circ \end{bmatrix} \\= \begin{bmatrix}\cos 8^\circ & \sin 8^\circ \\-\sin 8^\circ & \cos 8^\circ \end{bmatrix}^3 \begin{bmatrix}\cos 4^\circ & \sin 4^\circ \\-\sin 4^\circ & \cos 4^\circ \end{bmatrix}  \begin{bmatrix}\cos 2^\circ & \sin 2^\circ \\-\sin 2^\circ & \cos 2^\circ \end{bmatrix} \\= \begin{bmatrix}\cos 16^\circ & \sin 16^\circ \\-\sin 16^\circ & \cos 16^\circ \end{bmatrix} \begin{bmatrix}\cos 8^\circ & \sin 8^\circ \\-\sin 8^\circ & \cos 8^\circ \end{bmatrix} \begin{bmatrix}\cos 4^\circ & \sin 4^\circ \\-\sin 4^\circ & \cos 4^\circ \end{bmatrix}  \begin{bmatrix}\cos 2^\circ & \sin 2^\circ \\-\sin 2^\circ & \cos 2^\circ \end{bmatrix} \\= \begin{bmatrix}\cos 24^\circ & \sin 24^\circ \\-\sin 24^\circ & \cos 24^\circ \end{bmatrix}  \begin{bmatrix}\cos 6^\circ & \sin 6^\circ \\-\sin 6^\circ & \cos 6^\circ \end{bmatrix} = \begin{bmatrix} \cos 30^\circ & \sin 30^\circ \\-\sin 30^\circ & \cos 30^\circ \end{bmatrix} =\begin{bmatrix}\sqrt 3/2 & 1/2 \\-1/2 & \sqrt 3/2 \end{bmatrix}\\ \Rightarrow BA= \begin{bmatrix}\sqrt 3/2 & 1/2 \\-1/2 & \sqrt 3/2 \end{bmatrix} \begin{bmatrix}\sqrt 3/2 & \sqrt 3 \\ 1/2 & -3 \end{bmatrix} =\begin{bmatrix}1 & 0 \\0 & -2\sqrt 3 \end{bmatrix} \\ \Rightarrow \begin{bmatrix}x' \\y' \end{bmatrix}= BA \begin{bmatrix}x \\y \end{bmatrix} =\begin{bmatrix}x \\ -2\sqrt 3y \end{bmatrix} \Rightarrow \cases{x=x' \\ y=y'/-2\sqrt 3} \Rightarrow x'^2+({y'\over -2\sqrt 3})^2=1 \\ \Rightarrow x'^2+{y'^2\over 12}=1 \Rightarrow \bbox[red, 2pt]{\Gamma_2: x^2+{y^2\over 12}=1}$$

二、 計算證明題: 3 題(28 分)

解答： $$\textbf{(1)}\; a_n=3a_{n-1}+ 1 = 3(3a_{n-2}+1)+1=3^2a_{n-2}+3+1 =\cdots \\\qquad  =3^{n-1}a_1+3^{n-2}+ 3^{n-3}+ \cdots + 1 =3^{n-1}+3^{n-2}+ 3^{n-3}+ \cdots + 1  \\ \qquad={3^n-1\over 2} \Rightarrow \bbox[red, 2pt]{a_n={3^n-1\over 2},n\in \mathbb N }$$

解答： $$\cases{ab-{11\over 6}b=-1 \Rightarrow a={11\over 6}-{1\over b}\\ bc-{9\over 4}c=-1 \Rightarrow b={9c-4\over 4c}} \Rightarrow a={11\over 6}-{4c\over 9c-4} \\ ac-{8\over 3}a=-1 \Rightarrow a(c-{8\over 3})=-1 \Rightarrow \left({11\over 6}-{4c\over 9c-4} \right) \left(c-{8\over 3} \right)=-1 \\ \Rightarrow {75c-44\over 54c-24} \times {3c-8\over 3}=-1 \Rightarrow (75c-44)(3c-8)=-3(54c-24) \\ \Rightarrow 45c^2-114c+56=0 \Rightarrow (3c-2)(15c-28)=0 \Rightarrow c=\bbox[red, 2pt]{{2\over 3},{28\over 15}}$$

解答：$$自已看吧\to 參考資料$$

========================= END ====================

解題僅供參考，其他歷年試題及詳解