113年文華高中教甄-數學詳解

臺中市立文華高級中等學校 113 學年度第 1 次教師甄選數學科專業知能試題本

一、填充題： (共 80 分)
Ⅰ .填充一(每格 4 分，共 32 分， 每格全對才給分。 )

解答:$$f(x)=x^{2024}=(x^2+1)(x-1)^2p(x)+r(x),餘式最多為3次式 \\因此r(x)=(ax+b)(x^2+1)+cx+d \Rightarrow r'(x)=a(x^2+1)+2x(ax+b)+c \\ \Rightarrow \cases{f(1)=r(1)\\ f(i)=r(i)\\ f'(1)=r'(1)} \Rightarrow \cases{1=2a+2b+c+d\\ 1=ci+d\\ 2024=4a+2b+c} \Rightarrow \cases{a=1012\\ b=-1012\\ c=0\\d=1} \\ \Rightarrow r(x)=(1012x-1012)(x^2+1)+1= \bbox[red, 2pt]{1212x^3-1012x^2+1012x-1011}$$

解答:$$a_n={a_{n-1}+a_{n-2} \over 2} \Rightarrow 2a_n=a_{n-1}+a_{n-2} \Rightarrow a_n-a_{n-1} =a_{n-2}-a_n=a_{n-2}-{a_{n-1}+a_{n-2} \over 2} \\= -{1\over2}(a_{n-1}-a_{n-2}) \Rightarrow a_n-a_{n-1}= -{1\over2}(a_{n-1}-a_{n-2}) \Rightarrow b_n=-{1\over 2}b_{n-1}, \cases{b_n=a_n-a_{n-1}\\ b_2=2-1=1} \\ \Rightarrow  b_n={1\over 4}b_{n-2}= \cdots=(-{1\over 2})^{n-2}b_2 =(-{1\over 2})^{n-2}  \\又\cases{b_n=a_n-a_{n-1}\\ b_{n-1}=a_{n-1}-a_{n-2} \\ \cdots \\ b_2=a_2-a_1} \Rightarrow b_n+b_{n-1}+\cdots +b_2=a_n-a_1 \\ \Rightarrow a_n= \sum_{k=2}^n (-{1\over 2})^{k-2}+1 \Rightarrow \lim_{n\to \infty} a_n= {1\over 1-(-1/2)}+1=\bbox[red, 2pt]{5\over 3}$$

解答:

$$\overline{PC}與\overline{QB}的交點稱為費馬點\text{Fermat Point}，因此\overline{PC}=\overline{QB} \href{https://chu246.blogspot.com/2022/05/111.html}{(填充第1題)}\\又\cases{\triangle PBC為正三角形\Rightarrow \overline{PB}= \overline{AB} \\ \triangle QAB為正三角形\Rightarrow \overline{QC}= \overline{AC}}\\ 三角形中線定理:\cases{\triangle PBC: \overline{PC}^2+ \overline{PB}^2= 2(\overline{PM}^2+ \overline{BM}^2) \\ \triangle QBC:\overline{QB}^2 +\overline{QC}^2= 2(\overline{QM}^2+\overline{BM}^2)} \\兩式相減 \Rightarrow \overline{PB}^2-\overline{QC}^2 =2(\overline{PM}^2- \overline{QM}^2) \Rightarrow \overline{AB}^2-\overline{AC}^2=2(18^2-14^2)= 256 \\ \Rightarrow \overline{BC}^2=16^2 \Rightarrow \overline{BC}=\bbox[red, 2pt]{16}$$

解答:

$$\angle DFA=\angle DEA=90^\circ \Rightarrow AEDF共圓,假設此外接圓圓半徑=R \Rightarrow \overline{AD}=2R\\ \triangle AEF: {\overline{EF}\over \sin \angle A} =2R \Rightarrow \overline{EF}=2R\sin \angle A =\overline{AD} \sin \angle A\\ \Rightarrow \overline{EF}的最小值取決於\overline{AD},因此當\overline{AD} \bot \overline{BC}時,有最小的\overline{EF}\\ \triangle ABC:\cos \angle A= {5^2+6^2-7^2 \over 2\cdot 5\cdot 6}={1\over 5} \Rightarrow \sin \angle A={2\sqrt 6\over 5}\\ \Rightarrow \triangle ABC={1\over 2}\cdot 5\cdot 6\cdot {2\sqrt 6\over 5}=6\sqrt 6 = {1\over 2}\overline{AD} \cdot \overline{BC} \Rightarrow \overline{AD}= {12\sqrt 6\over 7} \\\Rightarrow \overline{EF}=\overline{AD} \sin \angle A= {12\sqrt 6\over 7} \cdot {2\sqrt 6\over 5} =\bbox[red, 2pt]{144\over 35}$$

解答:$$假設\cases{\overrightarrow{OA} =\vec a\\\overrightarrow{OB} =\vec b}  \Rightarrow \left|(1-t) \vec a+ 2t\vec b \right|\ge \sqrt 2  \Rightarrow ((1-t) \vec a+ 2t\vec b) \cdot ((1-t) \vec a+ 2t\vec b)\ge 2 \\ \Rightarrow (1-t)^2|\vec a|^2+4t(1-t) \vec a\cdot \vec b+4t^2|\vec b|^2 =4(1-t)^2+ 4t(1-t) \vec a\cdot \vec b+ 16t^2 \ge 2  \Rightarrow \vec a\cdot \vec b\ge 5+{6t+1\over 2t^2-2t}\\ 令f(t)={6t+1\over 2t^2-2t} \Rightarrow f'(t) =-{6t^2+2t-1\over 2t^2(t-1)^2} =0 \Rightarrow t={-1\pm \sqrt 7\over 6} \Rightarrow \cases{f((-1+\sqrt 7)/6) =-4-\sqrt 7 \\ f((-1-\sqrt 7)/6) =-4+\sqrt 7} \\ \Rightarrow 5+(-4-\sqrt 7)\le \vec a\cdot \vec b\le 5+(-4+\sqrt 7) \Rightarrow \bbox[red, 2pt]{]1-\sqrt 7\le \overrightarrow{OA} \cdot \overrightarrow{OB} \le 1+\sqrt 7}$$

解答:$$I_1＝\int_{-1}^7 \sqrt{-x^2+6x+7}\,dx = \int_{-1}^7 \sqrt{16-(x-3)^2}\,dx =8\pi \\y=\sqrt{16-(x-3)^2} \Rightarrow (x-3)^2+y^2=16為一圓\Rightarrow I_1=半圓面積=8\pi \\ I_2= \int_{-1}^7-2\,dx =-16\\ \Rightarrow 原式=I_1+I_2= \bbox[red, 2pt]{-16+8\pi}$$

解答:

$$7點共線有1條、4點共線有1條、5點共線有2條、3點共線有5條\Rightarrow 共9條\\ \cases{m=C^{17}_2- C^7_2-C^4_2-2C^5_2-5C^3_2+9=83\\ n=C^{17}_3-C^7_3-C^4_3-2C^5_3-5C^3_3=616} \Rightarrow m+n=\bbox[red, 2pt]{699}$$

解答:

$$假設\cases{L_1:3x+4y=10\\ L_2:4x+3y=10} \Rightarrow \cases{A=L_1\cap L_2=({10\over 7}, {10\over 7})\\ B=L_2\cap (y=0)=({5\over 2},0)\\ C=L_1\cap (y=0) =({10\over 3},0)} \\\Rightarrow \triangle ABC={1\over 2}({10\over 3}-{5\over 2})\cdot {10\over 7}= {25\over 42} \\ 欲求之面積=圓形+8\triangle ABC =4\pi+8\cdot {25\over 42}=\bbox[red, 2pt]{4\pi+{100\over 21}}$$

Ⅱ .填充二(每格 6 分，共 48 分， 每格全對才給分)

解答:$${1\over a_1a_2} +{1\over a_2a_3} +{1\over a_3a_4} + \cdots +{1\over a_{112}a_{113}} \\=\cfrac{{1\over a_1}-{1\over a_2}}{a_2-a_1} + \cfrac{{1\over a_2}-{1\over a_3}}{a_3-a_2} + \cfrac{{1\over a_3}-{1\over a_4}} {a_4-a_3} +\cdots +\cfrac{{1\over a_{112}}-{1\over a_{113}}}{a_{113}-a_{112}}  \\={1\over d}\left( {1\over a_1}-{1\over a_2}+{1\over a_2}-{1\over a_3} +{1\over a_3}-{1\over a_4}+ \cdots +{1\over a_{112}}-{1\over a_{113}}\right) ={1\over d}\left( {1\over a_1}-{1\over a_{113}}\right) \\={1\over d}\left( {1\over 1}-{1\over 1+112d}\right) ={112 \over 1+112d} =n \in \mathbb N \Rightarrow 1+112d={112\over n} \\ 依題意:d\gt 0 \Rightarrow 1+112d ={112\over n}\gt 1 \Rightarrow n=1,2,\dots,111 \\ \Rightarrow n=111有最小的d值=\frac{{112\over 111}-1}{112} ={1\over 111\times 112}= \bbox[red, 2pt]{1\over 12432}$$

解答:$$\sqrt{2x^2-6x+9} =\sqrt{x^2+x^2-6x+9} =\sqrt{(x-0)^2 +(x-3)^2} =\overline{OA}, 其中 \cases{O(0,0)\\ A(x,x-3)} \\ \sqrt{2x^2-16x+(\log_3 x)^2-2x\log_3 x+4\log_3 x+40}=\sqrt{(x-6)^2+(\log_3 x-x+2)^2} \\=\overline{AB}, 其中 B=(6,\log_3 x-1) \\因此f(x)= \overline{OA}+ \overline{AB} \le \overline{OB} =\sqrt{36+(\log_3x -1)^2} \Rightarrow 最小值=f(3)=\sqrt{36}=\bbox[red, 2pt] 6$$

解答:

$$f(x)=(1+x)^{1000}= \sum_{k=0}^{1000}C^{1000}_k x^k \Rightarrow f'(x)=1000(1+x)^{999}= \sum_{k=1}^{1000} k C^{1000}_k x^{k-1} \\ \Rightarrow xf'(x)=1000x(1+x)^{999} =\sum_{k=1}^{1000} k C^{1000}_k x^k \\ x=1 代入上式\Rightarrow 1000\cdot 2^{999}=\sum_{k=1}^{1000} k C^{1000}_k =P \Rightarrow \log P=3+999\times 0.301=303.699 \\ \Rightarrow \log P=303+\log 5 =\log (5\times 10^{303}) \Rightarrow P=5\times 10^{303} \Rightarrow \cases{a=5\\ b=0\\ c=304} \Rightarrow z=5\\ |\omega +7+5i| =|\omega-(-7-5i)|=1 \Rightarrow A(\omega)在圓:(x+7)^2+(y+5)^2=1上,\\ 而B(z)=(5,0) \Rightarrow \overline{AB} 之最小值=B至圓心O(-7,-5)的距離-圓半徑=13-1=12 \\ \Rightarrow \overline{AB}+c之最小值=12 +304= \bbox[red, 2pt]{316}$$

解答:$$把最後的比值想像成3,4,\dots,8,六個數字放在{1\over 2}的分子或分母,\\六個數字不是在分母就是在分子,共有2^6=64種排法\\ 由於3\times 8=4\times 6,也就是當\\狀況一:3,8同在分母,4,6同在分子\\狀況二:3,8同在分子,4,6同在分母\\剩下的5與7共有2^2=4種組合在狀況一或狀況二其比值是相同的,也就是有4種比值重複,\\因此最 後的結果是64-4=\bbox[red, 2pt]{60}$$

解答:$$\cases{A=\sqrt 2\begin{bmatrix}\cos (\pi/4) & -\sin(\pi/4) \\ \sin(\pi/4) & \cos(\pi/4) \end{bmatrix} \\[1ex]B=2 \begin{bmatrix}\cos(\pi/6) & -\sin(\pi/6) \\ \cos(\pi/6) & \sin(\pi/6) \end{bmatrix}} \\ A^\alpha B^\beta =2^{8-\gamma} I \Rightarrow \cases{\alpha \pi/4+\beta\pi/6 =2k\pi \Rightarrow 3\alpha +2\beta= 24k,k=1,2,\dots \cdots(1)\\ \alpha/2+\beta= 8-\gamma \ge 0\cdots(2)} \\ \begin{array}{} & k=1 &k=2 \\\hline (\alpha,\beta, \gamma) & (2, 9, \times) & (2,21,\times) \\ & (4,6,\times) & (4,18,\times)\\ &(6,3,2) & (6, 15,\times) \\ &(8,\times,\times) & (8,12,\times)\end{array} \\ \Rightarrow (\alpha,\beta,\gamma) = \bbox[red, 2pt]{(6,3,2)}$$

解答:$$f(x,y)=(x+y)^{16} =\sum_{k=0}^{16} C^{16}_k x^ky^{16-k} \Rightarrow \frac{\partial }{\partial x} f(x,y)=g(x,y)=16(x+y)^{15} =\sum_{k=1}^{16} kC^{16}_k x^{k-1}y^{16-k} \\ \Rightarrow  xg(x,y)=16x(x+y)^{15} =\sum_{k=1}^{16} kC^{16}_k x^{k}y^{16-k}  \\\Rightarrow  \frac{\partial }{\partial x} (xg(x,y)) =h(x,y)= 16(x+y)^{15}+16\cdot 15x(x+y)^{14} =\sum_{k=1}^{16} k^2C^{16}_k x^{k-1} y^{16-k} \\ \Rightarrow xh(x,y)=p(x,y)=16x(x+y)^{15}+16\cdot 15 x^2(x+y)^{14} =\sum_{k=1}^{16} k^2C^{16}_k x^{k}y^{16-k}  \\ \Rightarrow p({1\over 4},{3\over 4}) =16\cdot {1\over 4}\cdot 1+16\cdot 15\cdot {1\over 4^2}\cdot 1=4+15= \bbox[red, 2pt]{19}$$

解答:

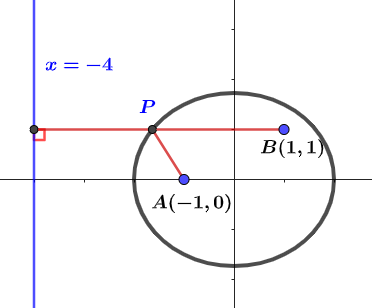
$${x^2 \over 4}+{y^2\over 3} =1 \Rightarrow \cases{a=2\\ b=\sqrt 3\\ c=1} \Rightarrow \cases{離心率e= c/a= 1/2 \\ 準線L:x=-a^2/c=-4} \Rightarrow e={\overline{PA} \over d(P,L)} ={1\over 2}\\ \Rightarrow 2\overline{PA} =d(P,L) \Rightarrow 2\overline{PA}+\overline{PB}的最小值發生在\overleftrightarrow{PB} \bot L,即\overleftrightarrow{PB} \parallel x軸\\ \Rightarrow 2\overline{PA}+\overline{PB}的最小值 = d(B,L) =1-(-4)= \bbox[red, 2pt]5$$

解答:$$\cases{L_1方向向量:\vec u_1=(1,2,-2) \\ L_2方向向量:\vec u_2=(-2,2,1) \\ L_3方向向量:\vec u_3=(2,1,2)  } \Rightarrow \vec u_1\times \vec u_2= (6,3,6) \parallel \vec u_3 \Rightarrow 三直線兩兩垂直互為歪斜線\\ 又\cases{P(3,6,-1) \in L_1\\ Q(2,7,4) \in L_2\\ R(1,5,6) \in L_3} \Rightarrow \cases{ \overrightarrow{PQ} =(-1,1,5) \\\overrightarrow{QR} =(-1,-2,2) \\\overrightarrow{RP} =(2,1,-7)} \Rightarrow \cases{d(L_1,L_2) ={\overrightarrow{PQ}\cdot \vec u_3 \over |\vec u_3|} =3 \\ d(L_2,L_3) ={\overrightarrow{QR}\cdot \vec u_1 \over |\vec u_1|} =3 \\ d(L_3,L_1) ={\overrightarrow{RP}\cdot \vec u_2 \over |\vec u_2|} =3 } \\ 因此此題可轉換成在稜長=3的立方體中,\cases{L_1=(a,0,3),a\in \mathbb R\\ L_2=(3,b,0),b\in \mathbb R\\ L_3=(0,3,c), c\in \mathbb R} \\ \Rightarrow \overline{PA}+ \overline{PB} =\sqrt{(a-3)^2+b^2+9} +\sqrt{a^2+9+(c-3)^2} ,\\因此最小值發生\cases{a=3/2\\ b=0\\ c=3} \Rightarrow  \overline{PA}+ \overline{PB} = \sqrt{45\over 4}+\sqrt{45\over 4} =\bbox[red, 2pt]{3\sqrt 5}$$

================ END =================

解題僅供參考，其他歷年試題及詳解