高雄市113學年度市立高級中等學校聯合教師甄選
一、 計算證明題 (1 至 7 題每題 4 分, 8 至 16 題每題 8 分,共 100 分
請寫下完整計算過程,否則不予計分。
解答:$$假設\beta=c+di,由於兩虛根成共軛複數, 因此 \beta^2+1=c-di\\ \Rightarrow (c+di)^2+1=c^2-d^2+1+2cdi =c-di \Rightarrow \cases{c^2-d^2+1=c\\ 2cd=-d} \Rightarrow \cases{c=-1/2\\d=\sqrt 7/2} \\ \Rightarrow 兩虛根為-{1\over 2}\pm {\sqrt 7i\over 2} ,同時也是 x^2+x +2=0的兩根 \\ \Rightarrow 3x^3+ax^2+bx-2=(x^2+x+2)(3x-1) =3x^3+ 2x^2+5x-2 \\ \Rightarrow (a,b)= \bbox[red, 2pt]{(2,5)}$$
解答:$$z=3-x-y \Rightarrow \cases{f(x,y)=x+y-2(3-x-y) =3x+3y-6\\g(x,y)=x^2+y^2+(3-x-y)^2-9 } \\ \Rightarrow \cases{f_x= \lambda g_x\\ f_y= \lambda g_y\\ g=0} \Rightarrow \cases{3= \lambda (4x+2y-6) \\ 3=\lambda (2x+4y-6)} \Rightarrow 2x+y=x+2y \Rightarrow x=y \\ \Rightarrow g(x,x)=0 \Rightarrow 2x^2+(3-2x)^2-9=0 \Rightarrow 6x^2-12x=0 \Rightarrow 6x(x-2)=0 \\ \Rightarrow \cases{x=0 \Rightarrow y=0 \Rightarrow z=3 \Rightarrow x+y-2z= -6\\ x=2 \Rightarrow y=2\Rightarrow z=-1 \Rightarrow x+y-2z=6} \Rightarrow (M,m)= \bbox[red, 2pt]{(6,-6)}$$
解答:$$\left(1+{1\over x} \right)^{x+1} =\left({x+1\over x} \right)^{x+1} =\left(({x\over x+1})^{-1} \right)^{x+1} = \left((1-{1\over x+1})^{-1} \right)^{x+1} \\=\left(1+{1\over -(x+1)} \right)^{-(x+1)} =\left( 1+{1\over 2024}\right)^{2024} \Rightarrow -(x+1)=2024 \Rightarrow x= \bbox[red, 2pt]{-2025}$$
解答:$$ \cases{\overrightarrow{OA}=(-5,4)\\ \overrightarrow{OB}=(6,9)} \Rightarrow \cases{C(-5s,4s) \\ D(6t,9t)} \Rightarrow 4s=9t \Rightarrow s={9\over 4}t \Rightarrow C(-{45\over 4}t,9t) \\ \Rightarrow \triangle OCD 面積=\triangle OAB面積 \Rightarrow \begin{Vmatrix}-{45\over 4}t &9t \\6t & 9t \end{Vmatrix} =\begin{Vmatrix}-5& 4\\ 6 & 9 \end{Vmatrix} \Rightarrow {621\over 4}t^2=69 \\ \Rightarrow t^2={4\over 9} \Rightarrow t={2\over 3} \Rightarrow \cases{C(-{15\over 2},6) \\D(4,6)} \Rightarrow \overline{CD}=4+{15\over 2}= \bbox[red, 2pt]{23\over 2}$$
解答:$$\cases{L_1:x+my=0\\ L_2:m(x-1)+3=y} \Rightarrow \cases{A(0,0)\\ B(1,3)\\ L_1\bot L_2 } \Rightarrow \overline{PA}\cdot \overline{PB}最大值出現在\overline{PA}= \overline{PB} \\ 假設\overline{PA}= a \Rightarrow 2a^2=\overline{AB}^2=10 \Rightarrow \overline{PA}\cdot \overline{PB}=a^2= \bbox[red, 2pt]5$$
解答:$$ 旋轉矩陣T=\begin{bmatrix}\cos 60^\circ & -\sin 60^\circ \\\sin 60^\circ & \cos 60^\circ \end{bmatrix} =\begin{bmatrix}1/2 & -\sqrt 3/2 \\\sqrt 3/2 & 1/2 \end{bmatrix} \\\begin{bmatrix}x' \\y' \end{bmatrix} =T\begin{bmatrix}x \\y \end{bmatrix} \Rightarrow \begin{bmatrix}x \\y \end{bmatrix} =T^{-1} \begin{bmatrix}x' \\y' \end{bmatrix} =\begin{bmatrix}\cos 60^\circ & \sin 60^\circ \\ -\sin 60^\circ & \cos 60^\circ \end{bmatrix} \begin{bmatrix}x' \\y' \end{bmatrix}= \begin{bmatrix}{1\over 2}(x'+\sqrt 3 y') \\ {1\over 2}(-\sqrt 3 x'+y') \end{bmatrix} \\ \Rightarrow x^2+ 2y^2= {1\over 4}(x'+\sqrt 3 y')^2+{2\over 4}(-\sqrt 3x'+y')^2=1 \Rightarrow 7x'^2-2\sqrt 3x'y'+5y'^2=4 \\ \Rightarrow \Gamma_2: \bbox[red, 2pt]{7x^2-2\sqrt 3xy+5y^2=4}$$
解答:$$\cases{L_1:(t,-t,-3t),t\in \mathbb R\\ L_2:(2+s,-1-2s,-s), s\in \mathbb R} \Rightarrow \cases{L_1方向向量 \vec u=(1,-1,-3)\\ L_2方向向量\vec v=(1,-2,-1) } \\ 假設P(t,-t,-3t)\in L_1在L_2的投影點為A(2+s,-1-2s,-s) \\\Rightarrow \overrightarrow{PA} =(2+s-t,-1-2s+t, -s+3t) \Rightarrow \overrightarrow{PA} \cdot \vec v=0 \Rightarrow s=t-{2\over 3} \\ \Rightarrow \overrightarrow{PA}=({4\over 3},-t+{1\over 3},2t+{2\over 3}) \Rightarrow |\overrightarrow{PA}| =\sqrt{5t^2+2t+{7\over 3}} =正\triangle 的高 \\ \Rightarrow \triangle 面積={\sqrt 3\over 3}| \overrightarrow{PA}|^2 = \bbox[red, 2pt]{{\sqrt 3\over 3}(5t^2+2t+{7\over 3})}$$
解答:$$\cases{\vec a=(-2,2,1) \\ \vec b=(1,3,2) \\ \vec c=(-2,3,1)} \Rightarrow \cases{\vec a\cdot \vec b=6\\ \vec b\cdot \vec c=9\\ \vec c\cdot \vec a=11 \\ |\vec a|^2=9\\ |\vec b|^2=14 \\ |\vec c|^2= 14} \Rightarrow |\vec a-s\vec b-t\vec c|^2 = (\vec a-s\vec b-t\vec c) \cdot (\vec a-s\vec b-t\vec c) \\ =f(s,t)=9+14s^2+ 14t^2-12s+18st-22t \Rightarrow \cases{f_s=28s+18t-12 =0\\ f_t=28t+18s-22=0} \\ \Rightarrow \cases{14s+9t=6\\ 9s+14t=11} \Rightarrow (s,t)=\bbox[red, 2pt]{\left( -{3\over 23},{20\over 23} \right)}$$
解答:
$$\angle B_1A_1O= \theta \Rightarrow \angle B_2A_2O= 2\theta \Rightarrow \cases{\overline{OB_2}=26\sin 2\theta\\ \overline{OA_2} = 26\cos 2\theta} \\\Rightarrow \triangle B_2A_2O ={1\over 2}\cdot 26\sin 2\theta \cdot 26\cos 2\theta =120 \Rightarrow \sin 4\theta ={120\over 169} \Rightarrow \cos 4\theta= \pm{119\over 169} \\ \Rightarrow \sin 2\theta= \sqrt{1-\cos 4\theta\over 2} ={5\over 13},{12\over 13}\Rightarrow \triangle B_1A_1O={1\over 2}\cdot 26\sin \theta \cdot 26\cos \theta=169\sin 2\theta \\ =\cases{169\cdot {5\over 13}=65\\ 169\cdot {12\over 13} =156} \Rightarrow \triangle B_1A_1O=\bbox[red, 2pt]{65,156}$$
解答:$$P=y+z \Rightarrow (x+y+z)^{2024}+ (x-y-z)^{2024}= (x+P)^{2024} +(x-P)^{2024} \\ =\sum_{n=0}^{2024} \left( C^{2024}_nP^nx^{2024-n} +C^{2024}_n(-P)^nx^{2024-n} \right) = \sum_{k=0}^{1012}C^{2024}_{2k}P^{2k}x^{2024-2k} \\ P^{2k}=(y+z)^{2k}有2k+1項 \Rightarrow \sum_{k=0}^{1012}C^{2024}_{2k}P^{2k}x^{2024-2k} 有1+3+5+ \cdots+2025 \\=1013^2= \bbox[red, 2pt]{1026169}$$
解答:$$\cases{\sin a+\sin b=\sqrt 2/2 \cdots(1)\\ \cos a+\cos b=\sqrt 6/2 \cdots(2)} \Rightarrow {(1)\over (2)}={\sin a+\sin b\over \cos a+\cos b} ={2\sin{a+b\over 2} \cos{a-b\over 2} \over 2\cos {a+b\over 2} \cos{a-b\over 2}}={1\over \sqrt 3} \\ \Rightarrow \tan {a+b\over 2}={1\over \sqrt 3} \Rightarrow \tan(a+b)={2\tan{a+b\over 2}\over 1-\tan^2{a+b\over 2}} = \sqrt 3 \Rightarrow \sin(a+b)=\bbox[red, 2pt]{\sqrt 3\over 2} \\ \bbox[cyan,2pt]{另解}:令複數\cases{z_1= \cos a+i \sin a\\ z_2= \cos b+i \sin b} \Rightarrow z=z_1+z_2= (\cos a+\cos b)+ i(\sin a+\sin b) ={\sqrt 6\over 2}+ i{\sqrt 2\over 2} \\ =\sqrt 2\left({\sqrt 3\over 2}+ i{1\over 2}\right) =\sqrt 2(\cos 30^\circ +i\sin 30^\circ) \Rightarrow {a+b\over 2}=30^\circ \Rightarrow a+b=60^\circ \Rightarrow \sin(a+b)=\bbox[red, 2pt] {\sqrt 3\over 2}\\ 參考資料: \href{http://www.math.nsysu.edu.tw/~problem/2008s/1ans.pdf}{中山大學雙週一題九十六學年度第二學期}$$
解答:
解答:$$P=y+z \Rightarrow (x+y+z)^{2024}+ (x-y-z)^{2024}= (x+P)^{2024} +(x-P)^{2024} \\ =\sum_{n=0}^{2024} \left( C^{2024}_nP^nx^{2024-n} +C^{2024}_n(-P)^nx^{2024-n} \right) = \sum_{k=0}^{1012}C^{2024}_{2k}P^{2k}x^{2024-2k} \\ P^{2k}=(y+z)^{2k}有2k+1項 \Rightarrow \sum_{k=0}^{1012}C^{2024}_{2k}P^{2k}x^{2024-2k} 有1+3+5+ \cdots+2025 \\=1013^2= \bbox[red, 2pt]{1026169}$$
解答:$$\cases{\sin a+\sin b=\sqrt 2/2 \cdots(1)\\ \cos a+\cos b=\sqrt 6/2 \cdots(2)} \Rightarrow {(1)\over (2)}={\sin a+\sin b\over \cos a+\cos b} ={2\sin{a+b\over 2} \cos{a-b\over 2} \over 2\cos {a+b\over 2} \cos{a-b\over 2}}={1\over \sqrt 3} \\ \Rightarrow \tan {a+b\over 2}={1\over \sqrt 3} \Rightarrow \tan(a+b)={2\tan{a+b\over 2}\over 1-\tan^2{a+b\over 2}} = \sqrt 3 \Rightarrow \sin(a+b)=\bbox[red, 2pt]{\sqrt 3\over 2} \\ \bbox[cyan,2pt]{另解}:令複數\cases{z_1= \cos a+i \sin a\\ z_2= \cos b+i \sin b} \Rightarrow z=z_1+z_2= (\cos a+\cos b)+ i(\sin a+\sin b) ={\sqrt 6\over 2}+ i{\sqrt 2\over 2} \\ =\sqrt 2\left({\sqrt 3\over 2}+ i{1\over 2}\right) =\sqrt 2(\cos 30^\circ +i\sin 30^\circ) \Rightarrow {a+b\over 2}=30^\circ \Rightarrow a+b=60^\circ \Rightarrow \sin(a+b)=\bbox[red, 2pt] {\sqrt 3\over 2}\\ 參考資料: \href{http://www.math.nsysu.edu.tw/~problem/2008s/1ans.pdf}{中山大學雙週一題九十六學年度第二學期}$$
解答:
$$\cases{\overline{AB}=2\\\overline{BC}=1\\ \overline{AC}=\sqrt 3} \Rightarrow \cases{\angle A=30^\circ\\ \angle B=60^\circ \\ \angle C=90^\circ} ,並假設\overline{EF}= \overline{DE}= \overline{DF}=a\\ \theta+\angle FED+\angle DEB=180^\circ = \angle BDE+\angle B+\angle DEB \\\Rightarrow \theta+60^\circ+ \angle DEB=\angle BDE+60^\circ+ \angle DEB \Rightarrow \angle BDE=\theta \\\cases{\triangle BDE: {a\over \sin 60^\circ} ={\overline{BE}\over \sin \theta} \\ \triangle FCE: \overline{CE}= a\sin \theta} \Rightarrow \overline{CE}+\overline{BE}= a\sin \theta+{2\over \sqrt 3}a \sin \theta=1 \\ \Rightarrow a={1\over \cos \theta+{2\over \sqrt 3}\sin \theta} ={1\over \sqrt{7\over 3}(\sqrt{3\over 7}\cos \theta+ {2\over \sqrt 7} \sin \theta)} = {1\over \sqrt{7\over 3} \sin(\theta+ \alpha)} \\ \Rightarrow 當\theta+ \alpha={\pi\over 2}時,a 有最小值,此時\sin \theta =\bbox[red, 2pt]{2\sqrt{7} \over 7}$$
解答:$$連續自然數列\langle a_n\rangle \Rightarrow a_n=a_1+(n-1)\\\log 2+\log(1+{1\over a_1}) +\log(1+{1\over a_2})+\cdots +\log(1+{1\over a_n})\\= \log 2+ \log(1+{1\over a_1}) + \log(1+{1\over a_1+1}) + \cdots +\log(1+{1\over a_1+(n-1)})\\= \log 2\cdot {a_1+1\over a_1}\cdot {a_1+2\over a_1+1}\cdots {a_1+n\over a_1+(n-1)}=\log2(1+{n\over a_1}) =\log n\\ \Rightarrow \\ \Rightarrow n={2\over 1-{2\over a_1}} \Rightarrow 當a_1=3時,n=6為最大值 \Rightarrow S_6=3+4+5+6+7+8 =\bbox[red, 2pt]{33}$$
解答:
解答:$$連續自然數列\langle a_n\rangle \Rightarrow a_n=a_1+(n-1)\\\log 2+\log(1+{1\over a_1}) +\log(1+{1\over a_2})+\cdots +\log(1+{1\over a_n})\\= \log 2+ \log(1+{1\over a_1}) + \log(1+{1\over a_1+1}) + \cdots +\log(1+{1\over a_1+(n-1)})\\= \log 2\cdot {a_1+1\over a_1}\cdot {a_1+2\over a_1+1}\cdots {a_1+n\over a_1+(n-1)}=\log2(1+{n\over a_1}) =\log n\\ \Rightarrow \\ \Rightarrow n={2\over 1-{2\over a_1}} \Rightarrow 當a_1=3時,n=6為最大值 \Rightarrow S_6=3+4+5+6+7+8 =\bbox[red, 2pt]{33}$$
解答:
$$z=x+yi \Rightarrow \text{Arg}(z+3)={3\over 4}\pi \Rightarrow (x+3, y)=k(\cos{3\over 4}\pi+i\sin {3\over 4}\pi) =k(-{\sqrt 2\over 2}+i{\sqrt 2\over 2})\\ \Rightarrow y=-(x+3) 為一直線L \Rightarrow P(z)\in L\\ 欲求{1\over |z-3i|+|z+6|}之最大值,相當於求|z-3i|+|z+6|之最小值\\ 而|z-3i| + |z +6|= \overline{AP}+ \overline{BP}, 其中\cases{A(0,3)\\ B(-6,0)} \Rightarrow \overline{AP} +\overline{BP} =\overline{AB}=3\sqrt 5為最小值\\ \Rightarrow {1\over |z-3i|+|z+6|}之最大值={1\over 3\sqrt 5}=\bbox[red, 2pt]{\sqrt 5\over 15}$$
解答:$$假設\cases{S0:數字為3的倍數\\ S1:數字除以3餘1 \\ S2:數字除以3餘2} \Rightarrow \cases{P(S0\to S0)=2/7\\ P(S1\to S0)=2/7\\ P(S2\to S0) = 3/7 \\P(S0\to S1)=3/7\\ P(S1\to S1)=2/7\\ P(S2\to S1)= 2/7 \\P(S0\to S2)=2/7\\ P(S1\to S2)=3/7\\ P(S2\to S_2)=2/7} \Rightarrow 轉移矩陣A={1\over 7}\begin{bmatrix}2 & 2 &3 \\3 & 2& 2\\ 2& 3& 2 \end{bmatrix} \\ B=\begin{bmatrix}2 & 2 &3 \\3 & 2& 2\\ 2& 3& 2 \end{bmatrix} =\begin{bmatrix}1 & \omega & \omega^2 \\1 & \omega^2 &\omega\\ 1 & 1& 1 \end{bmatrix} \begin{bmatrix}7 & 0& 0 \\0 & \omega^2 & 0\\ 0 & 0 & \omega \end{bmatrix} \begin{bmatrix}1/3 & 1/3 & 1/3 \\\omega^2/3 & \omega/3 & 1/3\\ \omega/3 & \omega^2/3& 1/3 \end{bmatrix} \\ \Rightarrow B^n={1\over 3} \begin{bmatrix}1 & \omega & \omega^2 \\1 & \omega^2 &\omega\\ 1 & 1& 1 \end{bmatrix} \begin{bmatrix}7^n & 0& 0 \\0 & \omega^{2n} & 0\\ 0 & 0 & \omega^n \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \\\omega^2 & \omega & 1\\ \omega & \omega^2 & 1 \end{bmatrix} \\= {1\over 3} \begin{bmatrix} 7^n+\omega^\left(2n \right)+ \omega^\left(n \right) & 7^n+ \omega^\left( n+ 1 \right) +\omega^\left(2n+2\right) & 7^n+ \omega^\left( n+2\right)+\omega^\left(2n+1\right) \\ 7^n+ \omega^\left(2n +1\right) +\omega^\left(n+ 2\right) & 7^n+ \omega^\left(2n \right) +\omega^\left(n \right) & 7^n+ \omega^\left(2n +2\right) +\omega^\left(n+ 1\right) \\ 7^n+ \omega^\left( 2n+2 \right)+ \omega^\left(n+1\right) & 7^n+ \omega^\left(n+ 2\right)+\omega^\left(2n+1\right) & 7^n+\omega^\left( 2n\right)+\omega^n \end{bmatrix} \\ \Rightarrow A^n={1\over 7^n}B^n \Rightarrow A^n \begin{bmatrix}1 \\0\\ 0 \end{bmatrix} =\begin{bmatrix} \alpha \\\beta \\\gamma \end{bmatrix} \Rightarrow \beta ={1\over 7^n} \cdot {1\over 3}(7^n+ \omega^{2n+ 1}+\omega^{n+2}) \\ \Rightarrow P_n= \bbox[red, 2pt]{{1\over 3}(1+{\omega^{2n+1}\over 7^n} +{\omega^{n+2}\over 7^n}),\omega=-{1\over 2}+{\sqrt 3\over 2}i}$$
解答:$$假設\cases{S0:數字為3的倍數\\ S1:數字除以3餘1 \\ S2:數字除以3餘2} \Rightarrow \cases{P(S0\to S0)=2/7\\ P(S1\to S0)=2/7\\ P(S2\to S0) = 3/7 \\P(S0\to S1)=3/7\\ P(S1\to S1)=2/7\\ P(S2\to S1)= 2/7 \\P(S0\to S2)=2/7\\ P(S1\to S2)=3/7\\ P(S2\to S_2)=2/7} \Rightarrow 轉移矩陣A={1\over 7}\begin{bmatrix}2 & 2 &3 \\3 & 2& 2\\ 2& 3& 2 \end{bmatrix} \\ B=\begin{bmatrix}2 & 2 &3 \\3 & 2& 2\\ 2& 3& 2 \end{bmatrix} =\begin{bmatrix}1 & \omega & \omega^2 \\1 & \omega^2 &\omega\\ 1 & 1& 1 \end{bmatrix} \begin{bmatrix}7 & 0& 0 \\0 & \omega^2 & 0\\ 0 & 0 & \omega \end{bmatrix} \begin{bmatrix}1/3 & 1/3 & 1/3 \\\omega^2/3 & \omega/3 & 1/3\\ \omega/3 & \omega^2/3& 1/3 \end{bmatrix} \\ \Rightarrow B^n={1\over 3} \begin{bmatrix}1 & \omega & \omega^2 \\1 & \omega^2 &\omega\\ 1 & 1& 1 \end{bmatrix} \begin{bmatrix}7^n & 0& 0 \\0 & \omega^{2n} & 0\\ 0 & 0 & \omega^n \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \\\omega^2 & \omega & 1\\ \omega & \omega^2 & 1 \end{bmatrix} \\= {1\over 3} \begin{bmatrix} 7^n+\omega^\left(2n \right)+ \omega^\left(n \right) & 7^n+ \omega^\left( n+ 1 \right) +\omega^\left(2n+2\right) & 7^n+ \omega^\left( n+2\right)+\omega^\left(2n+1\right) \\ 7^n+ \omega^\left(2n +1\right) +\omega^\left(n+ 2\right) & 7^n+ \omega^\left(2n \right) +\omega^\left(n \right) & 7^n+ \omega^\left(2n +2\right) +\omega^\left(n+ 1\right) \\ 7^n+ \omega^\left( 2n+2 \right)+ \omega^\left(n+1\right) & 7^n+ \omega^\left(n+ 2\right)+\omega^\left(2n+1\right) & 7^n+\omega^\left( 2n\right)+\omega^n \end{bmatrix} \\ \Rightarrow A^n={1\over 7^n}B^n \Rightarrow A^n \begin{bmatrix}1 \\0\\ 0 \end{bmatrix} =\begin{bmatrix} \alpha \\\beta \\\gamma \end{bmatrix} \Rightarrow \beta ={1\over 7^n} \cdot {1\over 3}(7^n+ \omega^{2n+ 1}+\omega^{n+2}) \\ \Rightarrow P_n= \bbox[red, 2pt]{{1\over 3}(1+{\omega^{2n+1}\over 7^n} +{\omega^{n+2}\over 7^n}),\omega=-{1\over 2}+{\sqrt 3\over 2}i}$$
======================== END =====================
主辦單位未公告答案,解題僅供參考
================== END =======================
解題僅供參考,歷年試題及詳解







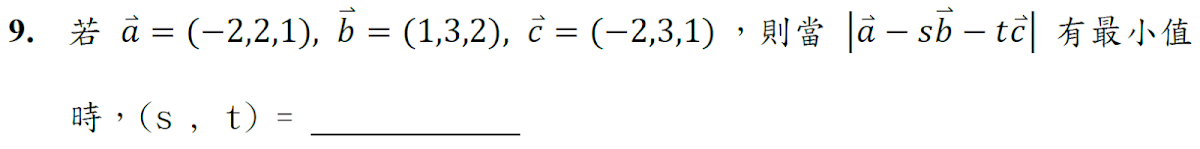










先點出已經有錯誤的部分(還未全部做過)
回覆刪除第1題,修正d_n,d_n=√1+4n^2-2n/√5(點到直線求距離),故答案應為1/4√5
第2題,因兩虛根分別為:(−1/2)±(√7i/2),這兩根為x^2+x+2=0的解,故(a,b)=(2,5)
謝謝!,已修訂,學校沒公告答案,但有人急著看,只能先這樣
刪除第十題 可能少考慮cos4倍角是負的
回覆刪除第十六題 答案誤植,與倒數第二行數值不同
第十題的cos4θ 也許是負的,但不影響結果,第十六題筆誤已修訂,謝謝!
刪除啊啊版主你講錯了,這題答案應該有兩個。
刪除如果cos4θ 是負的,後續利用半角公式算出sin2θ=12/13,會得到另一個答案156。
第10題應該有兩個答案156跟65,156出現在cos4倍角為負的情形
刪除謝謝,已修訂
刪除想請問一下,第16題第2列的算式是怎麼出現的呢?
回覆刪除用矩陣對角化來求矩陣的n次方
刪除了解了,謝謝老師
刪除第三題 (x^2+y^2)(1+1)>=(x+y)^2,然後全部代換z的不等式可求出z的範圍
回覆刪除請問12題不用考慮sin(a+b)為負的可能嗎
回覆刪除可以用sin(a+b)=2(tan((a+b)/2))/1+(tan((a+b)/2))^2,會發現只有一個解,這題出自於96年中山大學雙週一題
刪除感謝提供的資料, 中山大學【雙週一題】提供了三種解法,第二種解法就沒有sin(a+b) 為負的情形, 我再把它加到【另解】供大家參考!
刪除