國立臺灣海洋大學110學年度碩士班考試入學招生
考試科目:微積分
學系組名稱: 運輸科學系碩士班不分組
解答:$$\lim_{x \rightarrow 1} {x^2+x-2\over x^2-x} =\lim_{x \rightarrow 1} {(x+2)(x-1) \over x(x-1)} =\lim_{x \rightarrow 1} {x+2\over x} = \bbox[red, 2pt] 3$$解答:$$\lim_{x \rightarrow 0} {\sqrt{x^2+100}-10 \over x^2} =\lim_{x \rightarrow 0} { (\sqrt{x^2+100}-10)' \over (x^2)'} =\lim_{x \rightarrow 0} {{x\over \sqrt{x^2+100}} \over 2x} = \lim_{x \to 0} {1\over 2 \sqrt{x^2+100}} = \bbox[red, 2pt]{1\over 20}$$
解答:$$y={x^2+e^x \over x} \Rightarrow \frac{\text{d}y}{\text{d}x} ={2x+e^x \over x} -{x^2+e^x \over x^2} = \bbox[red, 2pt]{{ x^2+xe^x-e^x\over x^2}}$$
解答:$$\left( {f\over g}\right)'(x)={f'(x)\over g(x)} +f(x) \cdot \left( {1\over g(x)}\right)' ={f'(x)\over g(x)} -f(x)\cdot {g'(x)\over g^2(x)} ={g(x)f'(x)-f(x)g'(x) \over g^2(x)}, \bbox[red, 2pt]{QED}$$
解答:$$\frac{\text{d}(\tan x)}{\text{d} x} =\frac{\text{d} }{\text{d} x}{\sin x\over \cos x} ={(\sin x)'\over \cos x} +\sin x\left({1\over \cos x}\right)' ={\cos x\over \cos x}+ {\sin^2 x \over \cos^2 x} 1+\tan^2 x= \bbox[red, 2pt]{\sec^2 x}$$
解答:$$\ln x^r=\ln(\overbrace{x\cdot x\cdots x}^{r\, times})=\overbrace{\ln x+\ln x+\cdots +\ln x}^{r\; times} =r\ln x, \bbox[red, 2pt]{QED}$$
解答:$$u=x^3+x \Rightarrow du=(3x^2+1)dx \Rightarrow \int (x^3+x)^5(3x^2+1)dx = \int u^5du ={1\over 6}u^6+c \\ =\bbox[red, 2pt]{{1\over 6}(x^3+x)^6+c}$$
解答:$$\int_0^1 {dx\over x+1} = \left. \left[ \ln(x+1)\right] \right|_0^1 =\ln 2-\ln 1= \bbox[red, 2pt]{\ln 2}$$
解答:$$u=5x+1 \Rightarrow du=5dx \Rightarrow \int \sec^2(5x+1)\cdot 5dx = \int \sec^2 u\,du = \tan u+c=\bbox[red, 2pt]{\tan (5x+1)+c}$$
解答:$$u=x^3 \Rightarrow du=3x^2dx \Rightarrow \int x^2e^{x^3} dx = \int {1\over 3}e^{u} du = {1\over 3}e^u+c = \bbox[red, 2pt]{{1\over 3}e^{x^3}+c}$$
==================== END ======================
解題僅供參考,其他歷年試題及詳解



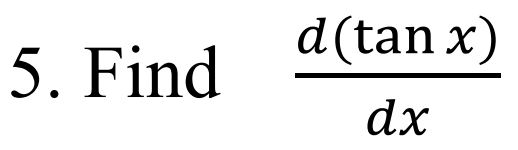

沒有留言:
張貼留言