113年嘉科實中國中部教甄-數學詳解

國立嘉科實驗高級中學113學年度國中部教師甄選

一、選擇題（每題4 分，共2 0 分）

解答: $$\cases{x^2+\sqrt 3y=4 \cdots(1)\\ y^2+\sqrt 3x=4 \cdots(2)} \Rightarrow x^2+\sqrt 3y=y^2+\sqrt 3x  \Rightarrow x^2-y^2=\sqrt 3x-\sqrt 3y\\ \Rightarrow (x+y)(x-y)=\sqrt 3(x-y) \Rightarrow x+y=\sqrt 3 \\ 又(1)+(2) \Rightarrow x^2+y^2+\sqrt 3(x+y)=8 \Rightarrow x^2+y^2+\sqrt 3\cdot \sqrt 3=8 \Rightarrow x^2+y^2=5 \\ 因此(x+y)^2= x^2+y^2+2xy \Rightarrow (\sqrt 3)^2 =5+2xy \Rightarrow xy=-1 \\ \Rightarrow {y\over x}+{x\over y}= {x^2+y^2\over xy} ={5\over -1}=-5, 故選\bbox[red, 2pt]{(D)}$$

解答: 

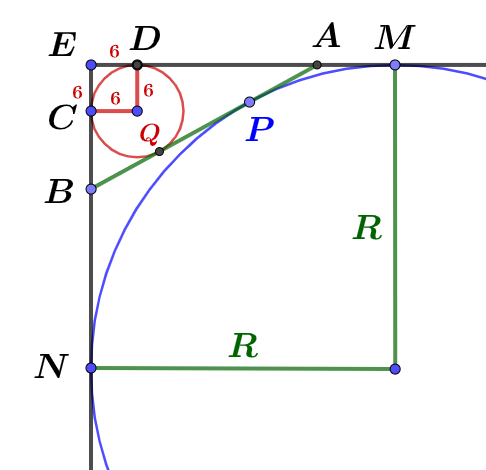
$$假設\overline{AB}在大圓的切點為P,小圖的切點為Q; 大圓的半徑為R,其它詳如上圖\\ 則\cases{R=\overline{EN}=6+\overline{BC}+\overline{BN} =6+\overline{BQ}+ \overline{BP} \cdots(1)\\ R= \overline{EM}= 6+ \overline{DA}+ \overline{AM}=6+\overline{AQ}+ \overline{AP}  \cdots(2)} \\ \Rightarrow (1)+(2) \Rightarrow 2R=12+(\overline{BQ}+ \overline{AQ})+ (\overline{BP}+ \overline{AP})= 12+\overline{AB}+ \overline{AB} \\ \Rightarrow 2R(正方形的邊長)=12+2\overline{AB} \Rightarrow 2R-2\overline{AB}=12, 故選\bbox[red, 2pt]{(A)}$$

解答: $$顯然h_b及h_c越大則面積越大,但h_b=\overline{BC}=10 \Rightarrow \angle C=90^\circ \Rightarrow \triangle ABC不是銳角三角形, 故選\bbox[red, 2pt]{(B)}$$

解答: $$m_8={1\over 2^8}(a_1+a_2) +{a_3\over 2^7} +{a_4\over 2^6} +{a_5\over 2^5} +{a_6\over 2^4} +{a_7\over 2^3} +{a_8\over 2^2}+{a_9\over 2} \\ \Rightarrow m_8要最大必須a_i=i,i=1-9 \\ \Rightarrow m_8={1\over 2^8}(1+2) +{3\over 2^7} +{4\over 2^6} +{5\over 2^5} +{6\over 2^4} +{7\over 2^3} +{8\over 2^2}+{9\over 2} ={2049\over 256}, 故選\bbox[red, 2pt]{(B)}$$

解答: 

$$即然沒有指定Q的條件,就假設Q在\overleftrightarrow{MO}與圓O的交點上,如上圖\\ \cases{T為切點\\ \overline{CQ}為直徑} \Rightarrow \angle MTQ=\angle CPQ=90^\circ \Rightarrow \sin \angle Q =\sin \theta={7\over 7+9+9} ={7\over 25} \\ \Rightarrow \cfrac{\overline{CQ}-\overline{CP}}{ \overline{PQ}} ={\overline{CQ}-\overline{CQ}\sin \theta \over \overline{CQ} \cos \theta} ={1-\sin \theta\over \cos \theta} =\cfrac{1-{7\over 25}}{24\over 25} ={18\over 24}=\bbox[red, 2pt]{3\over 4}$$

二、綜合題
(一) 填充題（每題7 分，共42 分）

解答:

$$y=x^2+2x-3=(x+3(x-1) \Rightarrow \cases{A(1,0) \\ B(-3,0)} \Rightarrow Q(2,y(2))=Q(2,5) \\\Rightarrow 對稱軸: x=(x(A)+x(B)\div 2) \Rightarrow x=-1 \Rightarrow Q的對稱點Q'=(-4,5) \\ \Rightarrow \overline{AQ'}: x+y=1 \Rightarrow P =(x=-1) \cap (x+y=1) =\bbox[red, 2pt]{(-1,2)}$$

解答: $$f(x)=2\cos^2 x+\sin(2x)-2\sin(2x)\cos(2x) =1+\cos(2x)+\sin(2x)-2\sin(2x)\cos(2x) \\ 令u=\cos(2x)+\sin(2x) \Rightarrow u^2=1+2\sin(2x) \cos(2x) \Rightarrow 2\sin(2x) \cos(2x)=u^2-1\\ \Rightarrow f(x)=g(u)=1+u-(u^2-1)=-u^2+u+2 \Rightarrow g'(u)=-2u+1=0 \Rightarrow u={1\over 2}\\但g({1\over 2})是極大值不是極小值,因此改取邊界值\\u=\cos(2x)+\sin(2x),0\le 2x\le 2\pi  \Rightarrow -\sqrt 2\le u\le \sqrt 2 \Rightarrow \cases{g(\sqrt 2)=-2+\sqrt 2+2=\sqrt 2\\ g(-\sqrt 2)=-2-\sqrt 2+2 =-\sqrt 2} \\ \Rightarrow 最小值為\bbox[red, 2pt]{-\sqrt 2}$$

解答: 

$$假設\overleftrightarrow{AD}與\overleftrightarrow{BC}交於點P,則\triangle ABP為一正三角形,因此若\overline{DP}=x,則\overline{CP}=x+2, 如上圖\\ \triangle PCD: \cos \angle P=\cos 60^\circ= {1\over 2}={x^2+(x+2)^2-12^2 \over 2x(x+2)} \Rightarrow x=\sqrt{141}-1\\ \Rightarrow \overline{AB}=x+10= \bbox[red, 2pt]{9+\sqrt{141}}$$

解答: $$2,3,\dots,2024有1012個偶數及1011個奇數,只要裁判選到偶數(假設是2k）\\ 將剩下的數,每連續兩個數分為同一組,\\即...,(2k-2,2k-1), (2k+1,2k+2), (2k+3,2k+4),...\\ 無論甲選到哪一個數,乙就選跟它同一組的數,最後就會剩下一組:兩個續續的整數\\ 兩個續續的整數一定是互質的,也就是乙獲勝, \\因此乙獲勝的機率就是裁判選到偶數的機率 = \bbox[red, 2pt]{1012\over 2023}$$

解答: $$n=11 \Rightarrow S(S(n))=S(2)=2\\ n= \overbrace{11 \cdots11}^{20個1}  \Rightarrow S(S(n))=S(20)=2 \\ n= \overbrace{11 \cdots11}^{200個1}  \Rightarrow S(S(n))=S(200)=2 \\ n= \overbrace{11 \cdots11}^{2000個1}  \Rightarrow S(S(n))=S(2000)=2\\ \dots \Rightarrow 有 \bbox[red, 2pt]{(無窮多個)}$$

解答: $$全-有1個共同語言+有2 個共同語言-有三個共同語言\\={5\choose 3}^4 -{5\choose 1}{4\choose 2}^4+ {5\choose 2}{3\choose 1}^4- {5\choose 3}= 10000-6480+ 810 -10 =\bbox[red, 2pt]{4320}$$

(二) 計算題（共18 分）

解答: $$\textbf{(1)}\; 用歸納法證明:\\\qquad n=1 \Rightarrow a_1=1顯然成立\\ \qquad n=2 \Rightarrow a_2=2+{1\over a_1}=3亦成立\\\qquad 假設n＝k時亦成立,即a_k = {\alpha_k\over \beta_k}, \alpha_k及\beta_k為互質的奇數\\ n=k+1 \Rightarrow a_{k+1}=2+{1\over a_k} =2+{\beta_k\over \alpha_k} ={2\alpha_k+ \beta_k\over \alpha_k} \Rightarrow (2\alpha_k+ \beta_k)與 \beta_kg 均為奇數且互質 \\\qquad \Rightarrow n=k+1亦成立, 因此原式成立\bbox[red, 2pt]{QED}\\ \textbf{(2)} \; 假設收斂值為a,則a=2+{1\over a} \Rightarrow a^2-2a-1=0 \Rightarrow a= \bbox[red, 2pt]{1+\sqrt 2 }, 其它再想想$$

三 申論題（共20 分）

=============== END =====================

解題僅供參考,其他歷年試題及詳解