基北區國立臺灣師範大學附屬高級中學
111 學年度高級中等學校特色招生考試
第一部分:單選題 (占 60 分)
解答:$$\cases{a\gt 0 \Rightarrow b\gt 0 \Rightarrow c\lt 0 \Rightarrow abc\lt 0 \Rightarrow {|abc|\over abc}+{|ab|\over ab}+ {|c|\over c}+1 = -1+ 1-1+1=0\\ a\lt 0 \Rightarrow b\lt 0 \Rightarrow c\gt 0 \Rightarrow abc \gt 0 \Rightarrow {|abc|\over abc}+{|ab|\over ab}+ {|c|\over c}+1 = 1+1+1+1=4}\\,故選\bbox[red, 2pt]{(4)}$$
解答:$$y=ax+b 通過(2,0) \Rightarrow 2a+b=0 \Rightarrow b=-2a;\\ax-b\gt 0 \Rightarrow ax\gt b\Rightarrow x\lt {b\over a} (因為a\lt 0) \Rightarrow x\lt {-2a\over a}=-2 \Rightarrow x\lt -2,故選\bbox[red, 2pt]{(3)}$$
解答:$$扣除相同的51,52,53,54,55,56,剩下數字的平方和\cases{卡1:1^2+2^2+3^2 = 14\\ 卡2: 2^2+3^2 +10^2 = 113\\ 卡3:3^2+10^2 +11^2 = 230\\ 卡4:10^2+11^2 +12^2 = 365} \\ \Rightarrow 卡3-卡2=230-113=117 \Rightarrow 剩下卡4-卡1=365-14=351,故選\bbox[red, 2pt]{(4)}$$
解答:
$$\angle A= 180^\circ-\angle B-\angle C=180^\circ-40^\circ-48^\circ =92^\circ \Rightarrow \angle DEF=180^\circ-\angle A=88^\circ (ADEF共圓)\\ \overline{DF} 為\angle ADE角平分線\Rightarrow \angle EDF=\angle FDA=\theta \Rightarrow \angle DFE=\theta (\overline{AB} \parallel \overline{EF}) \\\cases{ \triangle DEF: 2\theta+ 88^\circ=180^\circ \Rightarrow \theta = 46^\circ \\ \triangle ADF:\angle AFD= 180^\circ-92^\circ-\theta = 88^\circ-\theta}\Rightarrow \angle AFD= 88^\circ-46^\circ =42^\circ,故選\bbox[red, 2pt]{(1)}$$
解答:$$(A) \times:n=1\cdot 2\cdot 3\cdot 5 是10的倍數,但不是12的倍數\\(B)\times: n=1\cdot 2\cdot 3\cdot 4 是12的倍數,但不是10的倍數\\(C)\bigcirc: n為16=2^4的倍數\Rightarrow n=2\cdot 3\cdot 4\cdot 6 \Rightarrow n是9的倍數\\(D)\times: n=1\cdot 2\cdot 3\cdot 6 是9的倍數,但不是16的倍數\\,故選\bbox[red, 2pt]{(3)}$$
解答:$$\cases{A(0,0)\\ B(12,0)\\ C(20,15)} \Rightarrow \cases{\overline{BC}=17 \\\overline{AC}=25},令\overline{PC}=a \Rightarrow \overline{AB}=25-a=17+a \Rightarrow a=4\\ \Rightarrow \overline{AP}: \overline{PC}= 21:4 \Rightarrow P的x坐標={20\times 21\over 25} =16.8,故選\bbox[red, 2pt]{(2)}$$
解答:$$y=-2x^2+bx+c 通過(5,n)及(6,n-16) \Rightarrow \cases{n= -50+5b+c\\ n-16=-72+6b+c},兩式相減\Rightarrow 16=22-b\\ \Rightarrow b=6 \Rightarrow y=-2x^2+6x+c \Rightarrow 對稱軸:x={-6\over 2\cdot (-2)} ={3\over 2}=1.5,故選\bbox[red, 2pt]{(1)}$$
$$\overline{BA}= \overline{BD} \Rightarrow \angle BAD=\angle BDA =\theta ,又 \angle BAD+\angle C=90^\circ= \angle ADB+\angle EDC \\ \Rightarrow \theta +\angle C=\theta +\angle EDC \Rightarrow \angle C=\angle EDC \Rightarrow \overline{DE} =\overline{EC}=a \Rightarrow \overline{BE}=50-a\\ 在直角\triangle BDE中,20^2+a^2 =(50-a)^2 \Rightarrow 100a=2100 \Rightarrow a=21,故選\bbox[red, 2pt]{(2)}$$
$$\cases{\angle C=\angle E\\ \angle FBC+\angle HBF = \angle EBH+\angle HBF \Rightarrow \angle FBC=\angle EBH\\ \overline{BE} =\overline{BC}} \Rightarrow \triangle FBC\cong \triangle HBE (ASA)\\\Rightarrow \overline{HE} =\overline{FC}=3及\overline{AH}= \overline{DF}=2\\ 又\cases{\angle GFD=\angle FBC+\angle C \\ \angle GHA=\angle E+\angle HEB} \Rightarrow \angle GFB=\angle GHD 再加上\cases{\angle FGD=\angle HGA\\ \overline{AH}=\overline{DF}} \\ \Rightarrow \triangle HGA \cong \triangle GFD \Rightarrow \overline{GA}=\overline{GD} \Rightarrow \triangle BGA\cong \triangle BGD\\ 因此假設\triangle BGA面積=\triangle BGD面積=s \Rightarrow {\triangle GAH\over \triangle GAB}={\overline{AH} \over \overline{AB}} ={2\over 4} \Rightarrow \triangle GAH ={1\over 2}s \\\Rightarrow \triangle BDH=2s+{1\over 2}s= {5\over 2}s \Rightarrow {\triangle BHE\over \triangle BDH}={\overline{EH} \over \overline{HD}}={3\over 5} \Rightarrow \triangle BHE ={3\over 5}\cdot {5\over 2}s={3\over 2}s\\ \Rightarrow {灰色BDGA \over \triangle BDE}={2s \over {3s\over 2} +{5s\over 2}} ={1\over 2},故選\bbox[red, 2pt]{(1)}$$
解答:$$(a,b,c)=(-1,-4,0),(-1,-4,-2), (0,-3,-1), (0,-3,1), (1,-2,0), (1,-2,2), (2,-1,1),\\\qquad \qquad(2,-1,3),(3,0,2),共9組,故選\bbox[red, 2pt]{(2)}$$
解答:
解答:
$$假設P、Q、R為內切圓與三邊的切點 \Rightarrow \cases{\overline{AP} =\overline{AQ}\\ \overline{BQ}=\overline{BR} \\ \overline{CR}=\overline{CP}}; 假設\overline{AP}=a \Rightarrow \overline{BQ}=15-a = \overline{BR} \\ \Rightarrow \overline{CR}=17-(15-a)= 2+a = \overline{CP} \Rightarrow \overline{AC}=\overline{AP}+ \overline{CP} = a+ 2+a=18 \Rightarrow a=8\\ \triangle OQB \cong \triangle OPD (RHS) \Rightarrow \overline{PD}= \overline{QB}=15-a=7 \\\Rightarrow \overline{CD} =\overline{AC}-\overline{AP}-\overline{PD} =18-8-7=3,故選\bbox[red,2pt]{(3)}$$
解答:$$\begin{array} {c| ccccc|c} 球數 & 35 & 36 & 37 & 38 & 39 & 合計\\\hline 男生& 5-b & 4 & 4+b-a & 6 & a & 19\\ 女生& b & 4 & a-b-1 & 4& 4-a & 11\\\hline 合計 & 5 & 8 & 3 & 10 & 4 & 30\end{array} \\ 假設\cases{男生托球數由小至依序為a_1,a_2,\dots, a_{19}\\ 女生托球數由小至依序為b_1,b_2,\dots, b_{11}} \Rightarrow \cases{男生中位數a_{10}=38\\ 女生中位數b_{6}=36} \\ 由於\cases{b_6=36 \\ 女生托球數36及托球數38共8人} \Rightarrow \cases{b=2\\b=3}\\ 當b=2 \Rightarrow \begin{array} {c| ccccc|c} 球數 & 35 & 36 & 37 & 38 & 39 & 合計\\\hline 男生& 3 & 4 & 6-a & 6 & a & 19\\ 女生& 2 & 4 & a-3 & 4& 4-a & 11\\\hline 合計 & 5 & 8 & 3 & 10 & 4 & 30\end{array} ,再考慮a_{10}=38 \Rightarrow a=4\\ 當b=3 \Rightarrow \begin{array} {c| ccccc|c} 球數 & 35 & 36 & 37 & 38 & 39 & 合計\\\hline 男生& 2 & 4 & 7-a & 6 & a & 19\\ 女生& 3 & 4 & a-4 & 4& 4-a & 11\\\hline 合計 & 5 & 8 & 3 & 10 & 4 & 30\end{array} ,再考慮a_{10}=38 \Rightarrow a=4\\ 因此共有2組解,故選\bbox[red, 2pt]{(2)}$$
解答:$$,故選\bbox[red, 2pt]{(4)}$$
解答:$$a_{110}= \sum_{k=1}^{55}(2k-1)-\sum_{k=1}^{55} 2k = \sum_{k=1}^{55}(-1)=-55\\ a_{2021}=\sum_{k=1}^{1011}(2k-1)-\sum_{k=1}^{1010}2k =\sum_{k=1}^{1011}(2k-1)-\sum_{k=1}^{1011}2k +2022=-1011+2022=1011\\ 因此a_{110} +a_{2021} =-55+1011= \bbox[red, 2pt]{956}$$
解答:$$(a^b)^c =a^{b\times c} =\cases{2^{12} \Rightarrow (a=2,bc=12) \Rightarrow (a,b,c)=(2,1,12),(2,2,6), (2,3,4), (2,4,3), (2,6,2)\\\qquad,(2,12,1)\\4^6 \Rightarrow (a=4,bc=6) \Rightarrow (a,b,c)= (4,1,6),(4,2,3),(4,3,2), (4,6,1)\\ 8^4 \Rightarrow (a=8,bc=4) \Rightarrow (a,b,c)=(8,1,4),(8,2,2),(8,4,1) \\16^3 \Rightarrow (a=16,bc=3) \Rightarrow (a,b,c)=(16,1,3),(16, 3,1)\\ 64^2 \Rightarrow (a=64,bc=2) \Rightarrow (a,b,c)= (64,1,2),(64,2,1) \\ 4096^1 \Rightarrow (a=4096,bc=1) \Rightarrow (a,b,c)=(4096,1,1)} \\ \Rightarrow 共有6+4+ 3+2+2+1 =\bbox[red, 2pt]{18}組$$
解答:$$x=10a+b, 0\le a,b\le 9且a\ne 0 \Rightarrow {x\over f(x)} ={10a+b \over a+b}=10-{9b\over a+b} \\ \Rightarrow {9b\over a+b}要最大,因此取\cases{b=9\\ a=1} \Rightarrow x=\bbox[red, 2pt]{19}$$
解答:
解答:$$,故選\bbox[red, 2pt]{(4)}$$
第二部分:選填題 (占 40 分)
解答:$$x=0及x=20分別代入(x-20)f(x)-f(20-x)=20 \Rightarrow \cases{-20f(0)-f(20)=20 \cdots(1)\\ 0-f(0)=20 \cdots(2)} \\ 由(2) \Rightarrow f(0)=-20代入(1) \Rightarrow -20\cdot (-20)-f(20)= 20 \Rightarrow f(20)=400-20=\bbox[red, 2pt]{380}$$解答:$$a_{110}= \sum_{k=1}^{55}(2k-1)-\sum_{k=1}^{55} 2k = \sum_{k=1}^{55}(-1)=-55\\ a_{2021}=\sum_{k=1}^{1011}(2k-1)-\sum_{k=1}^{1010}2k =\sum_{k=1}^{1011}(2k-1)-\sum_{k=1}^{1011}2k +2022=-1011+2022=1011\\ 因此a_{110} +a_{2021} =-55+1011= \bbox[red, 2pt]{956}$$
解答:$$(a^b)^c =a^{b\times c} =\cases{2^{12} \Rightarrow (a=2,bc=12) \Rightarrow (a,b,c)=(2,1,12),(2,2,6), (2,3,4), (2,4,3), (2,6,2)\\\qquad,(2,12,1)\\4^6 \Rightarrow (a=4,bc=6) \Rightarrow (a,b,c)= (4,1,6),(4,2,3),(4,3,2), (4,6,1)\\ 8^4 \Rightarrow (a=8,bc=4) \Rightarrow (a,b,c)=(8,1,4),(8,2,2),(8,4,1) \\16^3 \Rightarrow (a=16,bc=3) \Rightarrow (a,b,c)=(16,1,3),(16, 3,1)\\ 64^2 \Rightarrow (a=64,bc=2) \Rightarrow (a,b,c)= (64,1,2),(64,2,1) \\ 4096^1 \Rightarrow (a=4096,bc=1) \Rightarrow (a,b,c)=(4096,1,1)} \\ \Rightarrow 共有6+4+ 3+2+2+1 =\bbox[red, 2pt]{18}組$$
解答:$$x=10a+b, 0\le a,b\le 9且a\ne 0 \Rightarrow {x\over f(x)} ={10a+b \over a+b}=10-{9b\over a+b} \\ \Rightarrow {9b\over a+b}要最大,因此取\cases{b=9\\ a=1} \Rightarrow x=\bbox[red, 2pt]{19}$$
解答:
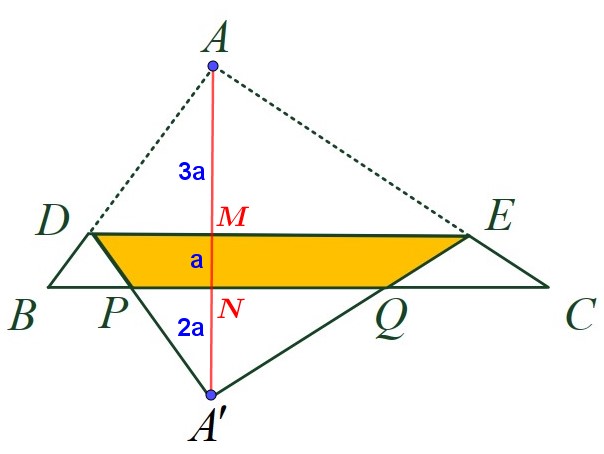
$$假設\overline{AA'}分別與\overline{DE}及\overline{PQ}交於M、N兩點,並令\overline{MN}=a,如上圖;\\\triangle A'DE重心在\overline{BC}上\Rightarrow \overline{A'N}=2a \Rightarrow \overline{AM}=a+2a=3a \Rightarrow \triangle ADE: \triangle ABC = 9:16 \\ \Rightarrow \triangle ADE = {9\over 16}\cdot 80 = 45 \Rightarrow \triangle A'DE= \triangle ADE=45;\\ 又\triangle A'PQ: \triangle A'DE = 4:9 \Rightarrow \triangle A'PQ ={4\over 9}\cdot 45 = 20 \Rightarrow 梯形DPQE = 45-20=\bbox[red, 2pt]{25}$$
$$T為半圓圓心,即\overline{PQ}中點 \Rightarrow 半圓半徑=\overline{TP} =\overline{TQ} =10\sqrt 3\div 2= 5\sqrt 3 \Rightarrow \overline{TC} =\overline{TD} = 5\sqrt 3\\ 假設\overline{QM}\bot \overline{TD} ,由於\angle CTD=90^\circ \Rightarrow \angle DTQ=\angle CTP = (180^\circ-90^\circ)\div 2=45^\circ \\\Rightarrow \overline{MQ}=\overline{MT} =5\sqrt 3\div \sqrt 2={5\over 2}\sqrt 6 \Rightarrow Q(5\sqrt 3+{5\over 2}\sqrt 6,5\sqrt 3-{5\over 2}\sqrt 6) \\ \Rightarrow 半圓半徑=\overline{OQ} = \sqrt{(5\sqrt 3+{5\over 2}\sqrt 6)^2 +(5\sqrt 3-{5\over 2}\sqrt 6)^2} =\sqrt{225}=\bbox[red,2pt]{15}$$
解答:$$a_n= (1,2,3,1),(2,3,1,2),(3,1,2,3) \Rightarrow a_{12}回到原點,共走了(1+2+3)\times 4= \bbox[red, 2pt]{24}個單位$$
解答:
解答:
$$作\overline{QT}\bot \overline{CD},見上圖;則\cases{\overline{QR}= \overline{AR}\\ \angle QTR=\angle RDA =90^\circ\\ \angle DAR+\angle DRA=90^\circ =\angle QRT+\angle DRA \Rightarrow \angle DAR=\angle QRT}\\ \Rightarrow \triangle ADR \cong \triangle RTQ (ASA) \Rightarrow \overline{RD} =\overline{QT} =a \Rightarrow \triangle DQR={1\over 2}\cdot \overline{RD} \cdot \overline{QT} \\ \Rightarrow 30={1\over 2}a^2 \Rightarrow a^2=60 \Rightarrow \overline{AR} =\sqrt{\overline{DR}^2+\overline{DA}^2} =\sqrt{60+100} =\sqrt{160} \\ \Rightarrow 正方形APQR面積= \overline{AR}^2 = \bbox[red,2pt]{160}$$
$$\overline{AB}為直徑\Rightarrow \angle ADB=90^\circ \Rightarrow \overline{BD} =\sqrt{10^2-8^2}=6 \Rightarrow \overline{BC} =\sqrt{\overline{BD}^2 +\overline{CD}^2} =\sqrt{6^2+2^2} =2\sqrt{10} \\ 又\cases{\overline{AB}為直徑\Rightarrow \angle AEB=90^\circ \\ \overline{AB}=\overline{AC}=10 \Rightarrow \triangle ABC為等腰} \Rightarrow \overline{AE}為\overline{BC}的中垂線 \Rightarrow \overline{AE}為\angle BAC的角平分線\\ \Rightarrow \overline{DE}= \overline{BE} ={1\over 2}\overline{BC} =\sqrt{\bbox[red,2pt]{10}}$$
解答:$$x為二位數\Rightarrow x=10-99 \Rightarrow 4x=40-396;\\又4x的十位數字為3 \Rightarrow 4x=130-139、230-239、330-339,但4x必須是4的倍數\\ \Rightarrow 4x=132,136,232, 236,332,336 \Rightarrow x=33,34,58,59,83,84;\\又6x的十位數字為4 \Rightarrow x=\bbox[red, 2pt]{58}$$
============================= END ===========================
============================= END ===========================
解題僅供參考,其他歷屆特招試題及詳解




















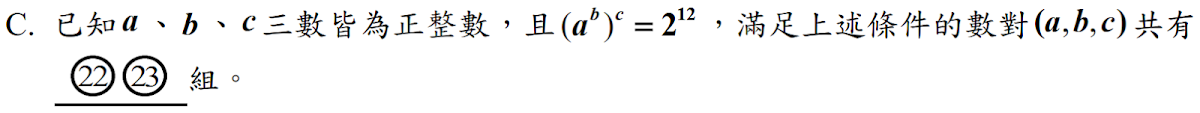










請問老師有選擇15的詳解嗎 謝謝~
回覆刪除老師,15錯誤囉,答案應該是(2)
回覆刪除附上學校公佈的答案,第15題答案是(4),不是(2),重點是算不出這個答案!!
刪除乙是 18, 甲是14 , 所以加起來是32
回覆刪除怎麼算的? 太久了, 都忘記還有這一題!
刪除