國立中央大學112學年度碩士班考試
所別: 光電類
科目: 工程數學
Choose the correct answer(50%): 單選題,每題5分
解答:$$I=I_0e^{-\alpha x } \Rightarrow {I\over I_0} ={1\over 10} =e^{-\alpha \times 0.46\times 10^{-4}} \Rightarrow \alpha\approx 5\times 10^4, 故選\bbox[red, 2pt]{(G)}$$解答:$$v=y^{-2} \Rightarrow v'=-2y^{-3}y' \Rightarrow y'=-{1\over 2}y^3v' 代回原式 \Rightarrow -{1\over 2}xy^3v'=y+e^xy^3 \\ \Rightarrow -{1\over 2}xv'={1\over y^2}+e^x =v+e^x \Rightarrow x^2v'+2xv=-2xe^x \Rightarrow (x^2v)'=-2xe^x \\ \Rightarrow x^2v= -2\int xe^x\,dx =-2(xe^x-e^x)+c \Rightarrow v={1\over y^2}=-2(x^{-1}e^x-x^{-2}e^x)+cx^{-2} \\ \Rightarrow y=(cx^{-2}- 2x^{-1} e^x +2x^{-2} e^x)^{-1/2}, 故選\bbox[red, 2pt]{(C)}$$
解答:$$\frac{\text{d}y}{\text{d}x} =\cfrac{2+ \sin x}{3(y-1)^2} \Rightarrow \int 3(y-1)^2\,dy = \int (2+\sin x)\,dx \Rightarrow (y-1)^3= 2x-\cos x+c_1\\ y(0)=1 \Rightarrow 0=-1+c_1 \Rightarrow c_1=1 \Rightarrow (y-1)^3= 2x-\cos x+ 1\\ \Rightarrow y=(2x-\cos x+1)^{1/3}+1, 故選\bbox[red, 2pt]{(B)}$$
解答:$$\frac{\text{d}R}{\text{d}t} =2R \Rightarrow R=c_1e^{2t},又R(0)=-1 \Rightarrow c_1=-1 \Rightarrow R=-e^{2t} \\ \Rightarrow R(1)=-e^2 =-7.389, 故選\bbox[red, 2pt]{(G)}$$
解答:$$1.9=2\times ({1\over 2})^{N} \Rightarrow N=0.074 \\\Rightarrow \text{ elapsed time =}0.074\times (1.4\times 10^{10}) =0.1036\times 10^{10}\text{ years}, 故選\bbox[red, 2pt]{(A)}$$
解答:$$3^{k/2} =2 \Rightarrow k=2\times \log_3 2 =1.2618, 故選\bbox[red, 2pt]{(C)}$$
解答:$$y=xv(x) \Rightarrow y'=v+xv' 代回原式 \Rightarrow x^2(v+xv')=x^2v^2-x^2v+x^2 \Rightarrow v+xv'=v^2-v+1 \\ \Rightarrow xv'=v^2-2v+1=(v-1)^2 \Rightarrow {dv\over (v-1)^2} ={dx \over x} \Rightarrow -{1\over v-1}=\ln x+ c_1 \\ \Rightarrow {1\over 1-{y\over x}} =\ln x+c_1 \Rightarrow {x\over x-y}=\ln x+c_1\\ y(1)=2 \Rightarrow {1\over 1-2}=0+c_1 \Rightarrow c_1=-1 \Rightarrow {x\over x-y}=\ln x-1 \\ x=2 \Rightarrow {2\over 2-y}=\ln 2-1 \Rightarrow y=2-{2\over \ln 2-1} =8.5178, 故選\bbox[red, 2pt]{(D)}$$
解答:$$\cases{P(x,y)=2x+2y^2\\ Q(x,y)=4xy+3y^2} \Rightarrow \frac{\partial P}{\partial y} =4y =\frac{\partial Q}{\partial x} \Rightarrow \text{Exact} \\ \Rightarrow \Phi(x,y)=\int P\,dx = \int Q \,dy \Rightarrow \int (2x+2y^2)\,dx = \int (4xy+3y^2)\,dy \\ \Rightarrow \Phi(x,y)=x^2+2xy^2+ \phi(y) = 2xy^2 +y^3+ \rho(x) \\ \Rightarrow x^2+2xy^2+y^3 =c_1\text{ constant}, 故選\bbox[red, 2pt]{(A)}$$
解答:$$\cases{P(x,y)=2x+1+2y^2\\ Q(x,y)=4xy+3y^2} \Rightarrow \frac{\partial P}{\partial y} =4y =\frac{\partial Q}{\partial x} \Rightarrow \text{Exact} \\ \Rightarrow \Phi(x,y)=\int P\,dx = \int Q \,dy \Rightarrow \int (2x+ 1+2y^2)\,dx = \int (4xy+3y^2)\,dy \\ \Rightarrow x^2+ x+2xy^2+ \phi(y) = 2xy^2 +y^3+ \rho(x) \Rightarrow \Phi=x^2+x+2xy^2+y^3 =c_1 \\ y(0)=-1 \Rightarrow c_1=-1 \Rightarrow x^2+x+2xy^2+y^3 +1=0 \\ \Rightarrow y=1 \Rightarrow x^2+x+2x+2=0 \Rightarrow x^2+3x+2=0 \Rightarrow (x+2)(x+1)=0 \\ \Rightarrow x=-2,-1, 故選\bbox[red, 2pt]{(D)}$$
解答:$$未給初始值, 其解常數項未知, 故選\bbox[red, 2pt]{(G)}$$
Solve the following problems (50%): 計算題(無計算過程者不予計分)
解答:$$\vec F(x,y,z)= (x-y, y-z,z-x) \Rightarrow \nabla\cdot \vec F = 1+1+1=3\\\text{By divergence theorem, } \iint_S \vec F\cdot \vec n\,dA = \iiint_R \nabla\cdot \vec F\,dV =\iiint_R 3\,dV \\= {4\over 3}\pi \cdot 3^3 \cdot {1\over 2}\cdot 3= \bbox[red, 2pt]{54\pi}$$解答:$$\textbf{(a)} \;A=\left[ \begin{matrix}1 & 3 & 1\\3 & 1 & 1\\1 & 1 & 3 \end{matrix} \right] \Rightarrow \det(A-\lambda I)=-(\lambda+2)(\lambda -2)(\lambda-5)=0 \Rightarrow \lambda=-2,2,5\\ \lambda_1=-2 \Rightarrow (A-\lambda_1 I)v=0 \Rightarrow \begin{bmatrix} 3 & 3 & 1 \\3 & 3 & 1 \\1 & 1 & 5\end{bmatrix} \begin{bmatrix} x_1\\x_2\\ x_3 \end{bmatrix} =0 \Rightarrow \cases{x_1+x_2=0\\ x_3=0} \\ \qquad \Rightarrow v=x_2\begin{pmatrix}-1\\ 1\\ 0 \end{pmatrix}, \text{choose }v_1= \begin{pmatrix} -1\\ 1\\ 0 \end{pmatrix} \\ \lambda_2=2 \Rightarrow (A-\lambda_2 I)v=0 \Rightarrow \begin{bmatrix} -1 & 3 & 1 \\3 & -1 & 1 \\1 & 1 & 1\end{bmatrix} \begin{bmatrix} x_1\\x_2\\ x_3 \end{bmatrix} =0 \Rightarrow \cases{2x_1+ x_3=0 \\ 2x_2+ x_3=0} \\ \qquad \Rightarrow v=x_3 \begin{pmatrix}-1/2\\ -1/2\\ 1 \end{pmatrix}, \text{choose }v_2= \begin{pmatrix}-1/2\\ -1/2\\ 1 \end{pmatrix}\\ \lambda_3=5 \Rightarrow (A-\lambda_3 I)v=0 \Rightarrow \begin{bmatrix} -4 & 3 & 1 \\3 & -4 & 1 \\1 & 1 & -2 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\ x_3 \end{bmatrix} =0 \Rightarrow \cases{x_1 =x_2\\ x_2=x_3} \\ \qquad \Rightarrow v=x_3 \begin{pmatrix}1\\ 1\\ 1 \end{pmatrix}, \text{choose }v_3= \begin{pmatrix}1\\ 1\\ 1 \end{pmatrix} \\ \Rightarrow X=[v_1 \mid v_2\mid v_3]\Rightarrow \bbox[red, 2pt]{X = \begin{bmatrix} -1 & \frac{-1}{2} & 1 \\1 & \frac{-1}{2} & 1 \\ 0 & 1 & 1 \end{bmatrix}}, \bbox[red, 2pt]{D=\begin{bmatrix}-2 & 0 & 0 \\0 & 2 & 0 \\0 & 0 & 5 \end{bmatrix}} \\\textbf{(b)} \;\left[\begin{matrix}1 & 3 & 1 & 1 & 0 & 0\\3 & 1 & 1 & 0 & 1 & 0\\1 & 1 & 3 & 0 & 0 & 1\end{matrix}\right] \xrightarrow{ R_2-3R_1\to R_2, R_3-R_1\to R_3} \left[ \begin{matrix}1 & 3 & 1 & 1 & 0 & 0\\0 & -8 & -2 & -3 & 1 & 0\\0 & -2 & 2 & -1 & 0 & 1\end{matrix}\right] \\ \quad \xrightarrow{ R_1 +1.5R_3\to R_1,R_2-4R_3\to R_2} \left[ \begin{matrix}1 & 0 & 4 & - \frac{1}{2} & 0 & \frac{3}{2}\\0 & 0 & -10 & 1 & 1 & -4\\0 & -2 & 2 & -1 & 0 & 1\end{matrix}\right] \xrightarrow{-R_2/10 \to R_2, -R_3/2\to R_3} \\\left[ \begin{matrix}1 & 0 & 4 & - \frac{1}{2} & 0 & \frac{3}{2}\\0 & 0 & 1 & - \frac{1}{10} & - \frac{1}{10} & \frac{2}{5}\\0 & 1 & -1 & \frac{1}{2} & 0 & - \frac{1}{2}\end{matrix}\right] \xrightarrow{R_2 \leftrightarrow R_3} \left[ \begin{matrix}1 & 0 & 4 & - \frac{1}{2} & 0 & \frac{3}{2}\\0 & 1 & -1 & \frac{1}{2} & 0 & - \frac{1}{2}\\0 & 0 & 1 & - \frac{1}{10} & - \frac{1}{10} & \frac{2}{5} \end{matrix} \right] \\ \xrightarrow{R_1-4R_3\to R_1, R_2+R_3\to R_2} \left[\begin{matrix}1 & 0 & 0 & - \frac{1}{10} & \frac{2}{5} & - \frac{1}{10}\\0 & 1 & 0 & \frac{2}{5} & - \frac{1}{10} & - \frac{1}{10}\\0 & 0 & 1 & - \frac{1}{10} & - \frac{1}{10} & \frac{2}{5}\end{matrix}\right] \Rightarrow \bbox[red, 2pt]{A^{-1} =\left[ \begin{matrix} - \frac{1}{10} & \frac{2}{5} & - \frac{1}{10}\\ \frac{2}{5} & - \frac{1}{10} & - \frac{1}{10}\\ - \frac{1}{10} & - \frac{1}{10} & \frac{2}{5} \end{matrix} \right]} \\\textbf{(c)} \;A=XDX^{-1} \Rightarrow A^{-1}=(XDX^{-1})^{-1} = XD^{-1} X^{-1} \Rightarrow \cases{Y=X\\ E=D^{-1}} \\ \Rightarrow \bbox[red, 2pt]{Y = \begin{bmatrix} -1 & \frac{-1}{2} & 1 \\1 & \frac{-1}{2} & 1 \\ 0 & 1 & 1 \end{bmatrix}}$$
解答:$$V=R\times i(t) +{1\over C}\int i(t)\, dt \Rightarrow L\{V\} = L\left\{ R\times i(t) +{1\over C}\int i(t)\, dt\right\} \\ \Rightarrow {V\over s}=R\cdot I(s) +{1\over C}\cdot {I(s)\over s} =(R+{1\over Cs})I(s) \Rightarrow I(s)= {V\over R}\cdot {1\over s+{1\over RC}} \\ \Rightarrow i(t)= L^{-1}\{ I(s)\} ={V\over R}\cdot L^{-1} \left\{ {1\over s+{1\over RC}} \right\} \Rightarrow i(t)={V\over R} e^{-t/RC} \\ \text{Given } \cases{V= 5\\ R=10K\Omega =10^4 \Omega \\ C=10\mu F= 10^{-5}F} \Rightarrow \bbox[red, 2pt]{i(t)=\cases{{5\over 10^4} e^{-10t},1\lt t\lt 3 \\ 0, \text{otherwise}}}$$
解答:$$\textbf{(a)}\; f_1(t)=\cos(2t) e^{-3|t|} \Rightarrow \mathcal F(f_1(t))={1\over \sqrt{2\pi}} \int_{-\infty}^\infty \cos(2t) e^{-3|t|} e^{-i\omega t}\,dt \\={1\over \sqrt{2\pi}} \left( \int_{-\infty}^0 \cos(2t)e^{3t} e^{-i\omega t}\,dt +\int_0^\infty \cos(2t) e^{-3t} e^{-i\omega t}\,dt\right) \\={1\over \sqrt{2\pi}} \left( \int_{-\infty}^0 \cos(2t)e^{(3-i\omega)t} \,dt +\int_0^\infty \cos(2t) e^{-(3+ i\omega)t} \,dt\right) \\={1\over 2\sqrt{2\pi}} \left( \int_{-\infty}^0 (e^{2it}+ e^{-2it}) e^{(3-i \omega)t} \,dt +\int_0^\infty (e^{2it}+ e^{-2it}) e^{-(3+i\omega)t} \,dt\right) \\={1\over 2 \sqrt{2 \pi}} \left( \int_{-\infty}^0 (e^{(3+(2-\omega)i) t}+ e^{(3-(2+\omega)i)t}) \,dt +\int_0^\infty (e^{-(3+(\omega-2)i)t}+ e^{-(3+ (\omega+2)i)t}) \,dt\right) \\={1\over 2\sqrt{2\pi}} \left( \left. \left[{1\over 3+(2-\omega)i} e^{(3+(2-\omega)i) t} +{1\over 3-(2+\omega)i} e^{(3- (2+ \omega)i)t} \right] \right|_{-\infty}^0 \right) \\\qquad + {1\over 2\sqrt{2\pi}} \left( \left.\left[{1\over -(3+(\omega-2)i)} e^{-(3+(\omega-2)i) t} +{1\over -(3+ (\omega+2)i)} e^{-(3+ (\omega+2)i)t} \right] \right|_0^{ \infty} \right) \\={1\over 2\sqrt{2\pi}} \left( {1\over 3+(2-\omega)i} +{1\over 3-(2+\omega)i} +{1\over 3+(\omega-2)i} +{1\over 3+ (\omega+2)i} \right)\\={1\over 2\sqrt{2\pi}} \left({6\over 9+(\omega+2)^2} +{6\over 9+(\omega-2)^2} \right) =\bbox[red, 2pt]{{3\over \sqrt{2\pi}} \left({1 \over 9+(\omega+2)^2} +{1\over 9+(\omega-2)^2} \right)} \\\textbf{(b)}\; f_2(t)=\delta(t+{1\over 2})-\delta(t-{1\over 2}) \Rightarrow \mathcal F(f_2(t))={1\over \sqrt{2\pi}} \int_{-\infty}^\infty (\delta(t+{1\over 2})-\delta(t-{1\over 2})) e^{-i\omega t}\,dt \\={1\over \sqrt{2\pi}}\left(e^{i\omega/2}-e^{-i\omega/2} \right) ={2\over \sqrt{2\pi}} i\sin(\omega/2) = \bbox[red, 2pt]{\sqrt{2\over \pi} i\sin{\omega \over 2}}$$
==================== END ==================
解題僅供參考, 其他歷年試題及詳解

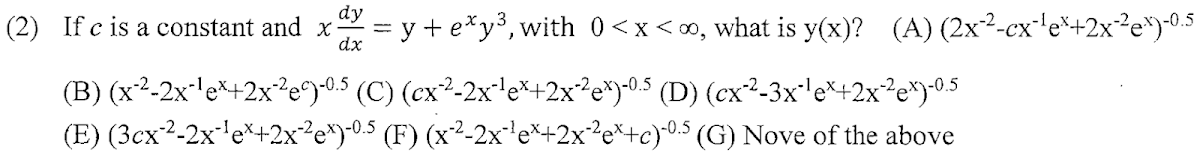











勘誤一下
回覆刪除1.第九題的積分(v-1)^-2那邊錯了少了負號,所以才沒答案(實際是有的)
2.12題的(c),E那個對角矩陣寫錯了(應該單純筆誤)
3.14題的(b),答案應該要多一個i.(e^(iw/2)-e(-iw/2)=2isin(w/2).)
更正第一部分是第7題
刪除謝謝再幫我驗算一遍,已更正完畢!!
刪除