103 學年度科技校院四年制與專科學校二年制
統一入學測驗 -數學(B)
解答：$$令f(x)=ax^2+px-6，並由題意可知:\cases{a=3\\ b=\sqrt 3-1} \Rightarrow f(x)=3x^2+px-6\\ 又 f(b)=0 \Rightarrow 3(\sqrt 3-1)^2+p(\sqrt 3-1)-6= (6-p)-\sqrt 3(6-p)=0 \Rightarrow p=6，故選\bbox[red,2pt]{(C)}$$
解答：$$\left| \begin{matrix} d & e & f \\ 1 & -2 & 3 \\ a & b & c \end{matrix} \right| =-\begin{vmatrix} e & f \\ b & c \end{vmatrix}-2\begin{vmatrix} d & f \\ a & c \end{vmatrix}-3\begin{vmatrix} d & e \\ a & b \end{vmatrix}\\ =\begin{vmatrix} b & c \\ e & f \end{vmatrix}+2\begin{vmatrix} a & c \\ d & f \end{vmatrix}+3\begin{vmatrix} a & b \\ d & e \end{vmatrix}，故選\bbox[red,2pt]{(B)}$$
解答：$$若二元一次方程式之二根為\alpha及\beta，則二根差之平方=(\alpha-\beta)^2= (\alpha+\beta)^2-4\alpha\beta\\ 因此\cases{x^2+ax+2=0 之二根差之平方=a^2-8\\ x^2+2x+a=0之二根差之平方=4-4a} \Rightarrow a^2-8=4-4a \\ \Rightarrow a^2+4a-12=0 \Rightarrow (a+6)(a-2)=0 \Rightarrow a=-6，故選\bbox[red,2pt]{(A)}$$
解答：$$令f(x)=x^3+kx-6，則f(3)=0 \Rightarrow 27+3k-6=0 \Rightarrow k=-7 \\ \Rightarrow f(x)=x^3-7x-6 =(x-3)(x^2+3x+2) = (x-3)(x+1)(x+2)，故選\bbox[red,2pt]{(D)}$$
解答：$$令f(x)=x^4-x^3-2x^2+13x+ k=(x^2+2x+a)(x^2-3x+b)\\ \Rightarrow \cases{f(0)= k=ab\\ f(1)=11+k= (3+a)(-2+b) \\ f(-1)= -13+k= (-1+a)(4+b)} \Rightarrow \cases{ab=k\\ 2a-3b=-17\\ 4a-b=-9} \Rightarrow \cases{a=-1\\ b=5\\ k=-5}，故選\bbox[red,2pt]{(A)}$$
解答：$$\frac { xy+yz+zx }{ 3 } \ge \sqrt [ 3 ]{ { \left( xyz \right) }^{ 2 } } ={ \left( xyz \right) }^{ 2/3 }\Rightarrow 9\ge { \left( xyz \right) }^{ 2/3 } \Rightarrow 3\ge { \left( xyz \right) }^{ 1/3 }\Rightarrow 27\ge xyz，故選\bbox[red,2pt]{(C)}$$
解答：$$f(x)=(x^2+2)^2 \Rightarrow f'(x)=2(x^2+2)(2x) \Rightarrow f'(1)=2\cdot 3\cdot 2=12\\而\lim _{ x\rightarrow 1 }{ \frac { f\left( x \right) -f\left( 1 \right) }{ x-1 } } = f'(1)=12，故選\bbox[red,2pt]{(D)}$$
解答：$$\int _{ \frac { 1 }{ \pi } }^{ \frac { 2 }{ \pi } }{ \left( { \pi }^{ 2 }x+\pi \right) dx } =\left.\left( \frac { 1 }{ 2 } { \pi }^{ 2 }{ x }^{ 2 }+\pi x \right) \right| _{ 1/\pi}^{2/\pi }=\left( 2+2 \right) -\left( \frac { 1 }{ 2 } +1 \right) =4-\frac { 3 }{ 2 } =\frac { 5 }{ 2 }，故選\bbox[red,2pt]{(A)}$$
解答：$$\frac { 3 }{ 5x+10 } <\frac { x }{ 5 } \Rightarrow \frac { 3 }{ 5x+10 } -\frac { x }{ 5 } <0\Rightarrow \frac { 3 }{ 5\left( x+2 \right) } -\frac { x\left( x+2 \right) }{ 5\left( x+2 \right) } <0\\ \Rightarrow \frac { 3-x\left( x+2 \right) }{ 5\left( x+2 \right) } <0\Rightarrow \frac { 3-{ x }^{ 2 }-2x }{ 5\left( x+2 \right) } <0\Rightarrow \frac { -\left( x+3 \right) \left( x-1 \right) }{ 5\left( x+2 \right) } <0\\ \Rightarrow \left( x-1 \right) \left( x+2 \right) \left( x+3 \right) >0\Rightarrow x>1,-3<x<-2，故選\bbox[red,2pt]{(D)}$$
解答：$$\frac { \log _{ 5 }{ \sqrt { 2 } } \cdot \log _{ 7 }{ 9 } }{ \log _{ 5 }{ \left( \frac { 1 }{ 3 } \right) } \cdot \log _{ 7 }{ \sqrt [ 3 ]{ 4 } } } =\frac { \frac { \frac { 1 }{ 2 } \log { 2 } }{ \log { 5 } } \cdot \frac { 2\log { 3 } }{ \log { 7 } } }{ \frac { -\log { 3 } }{ \log { 5 } } \cdot \frac { \frac { 2 }{ 3 } \log { 2 } }{ \log { 7 } } } =\frac { 1 }{ \frac { -2 }{ 3 } } =-\frac { 3 }{ 2 }，故選\bbox[red,2pt]{(B)}$$
解答：$${ 49 }^{ x }+5\cdot { 7 }^{ x }-24=0\Rightarrow { 7 }^{ 2x }+5\cdot { 7 }^{ x }-24=0\\ \Rightarrow \left( { 7 }^{ x }+8 \right) \left( { 7 }^{ x }-3 \right) =0\Rightarrow { 7 }^{ x }=3\Rightarrow { 7 }^{ x+1 }=21，故選\bbox[red,2pt]{(C)}$$
解答：
$$\cases{A(5,0)\\ B(1,-12)\\ C(-4,-7)\\ D(x,y)} \Rightarrow \cases{\overrightarrow{AB} =(-4,-12)\\ \overrightarrow{CD}= (x+4,y+7) \\ \overrightarrow{AD}=(x-5,y)}；\\由於\cases{\overrightarrow{AB} \bot \overrightarrow{CD}\\ \overrightarrow{AB} \parallel \overrightarrow{AD}} \Rightarrow \cases{(-4,-12)\cdot (x+4,y+7)=0\\ {1\over x-5}={3\over y}} \Rightarrow \cases{3x-y=15\\ x+3y=-25} \Rightarrow \cases{x=2\\ y=-9}\\ \Rightarrow x+y=2-9=-7，故選\bbox[red,2pt]{(D)}$$
解答：$$\tan { 2\theta =\frac { \sin { 2\theta } }{ \cos { 2\theta } } } =\frac { 2\sin { \theta } \cos { \theta } }{ 2\cos ^{ 2 }{ \theta } -1 } =\frac { 2\times \frac { 3 }{ 5 } \times \frac { 4 }{ 5 } }{ 2\times { \left( \frac { 4 }{ 5 } \right) }^{ 2 }-1 } =\frac { \frac { 24 }{ 25 } }{ \frac { 7 }{ 25 } } =\frac { 24 }{ 7 }，故選\bbox[red,2pt]{(D)}$$
解答：$$\frac { \sin { \theta } }{ \cos { \theta } } +\frac { \cos { \theta } }{ \sin { \theta } } =-\frac { 8 }{ 3 } \Rightarrow \frac { \sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } }{ \sin { \theta } \cos { \theta } } =-\frac { 8 }{ 3 } \\ \Rightarrow \frac { 1 }{ \sin { \theta } \cos { \theta } } =-\frac { 8 }{ 3 } \Rightarrow \sin { \theta } \cos { \theta } =-\frac { 3 }{ 8 } \\ { \left( \sin { \theta } +\cos { \theta } \right) }^{ 2 }=1+2\sin { \theta } \cos { \theta } =1+2\times \left( -\frac { 3 }{ 8 } \right) =\frac { 1 }{ 4 }，故選\bbox[red,2pt]{(A)}$$
解答：$$令D(a,b)，則\overrightarrow { AD } =\frac { 2 }{ 5 } \overrightarrow { AB } +\frac { 3 }{ 5 } \overrightarrow { AC } \Rightarrow (a-x,b-y)=\frac { 2 }{ 5 } \left( -1-x,4-y \right) +\frac { 3 }{ 5 } \left( 9-x,-1-y \right) \\ =\left( 5-x,1-y \right) \Rightarrow a=5,b=1，故選\bbox[red,2pt]{(C)}$$
解答：$$兩數相乘=0.8999999\cdots，故選\bbox[red,2pt]{(B)}$$
解答：$$\because \overrightarrow { a } \cdot \overrightarrow { b } =\left| \overrightarrow { a } \right| \left| \overrightarrow { b } \right| \cos { 60° } =\frac { 1 }{ 2 } \\ \therefore \overrightarrow { a } \cdot \left( -\overrightarrow { a } +2\overrightarrow { b } \right) =\left| \overrightarrow { a } \right| \left| -\overrightarrow { a } +2\overrightarrow { b } \right| \cos { \theta } \Rightarrow \cos { \theta } =\frac { -\overrightarrow { a } \cdot \overrightarrow { a } +2\overrightarrow { a } \cdot \overrightarrow { b } }{ \left| \overrightarrow { a } \right| \left| -\overrightarrow { a } +2\overrightarrow { b } \right| } =\frac { -1+1 }{ \left| -\overrightarrow { a } +2\overrightarrow { b } \right| } =0\\ \Rightarrow \theta =90°，故選\bbox[red,2pt]{(C)}$$
解答：$$此題相當於求x+y=2017的非負整數解個數，即H^2_{2017}=C^{2018}_{2017}= 2018，故選\bbox[red,2pt]{(A)}$$
解答：$${ 2 }^{ 5 }\cdot { 3 }^{ 7 }\cdot { 5 }^{ 11 }=8\cdot \left( { 2 }^{ 2 }\cdot { 3 }^{ 7 }\cdot { 5 }^{ 11 } \right)=8\cdot b \Rightarrow b可能有(2+1)(7+1)(11+1)= 288種數字組合\\，故選\bbox[red,2pt]{(B)}$$
解答：$$\cases{P(A')=1/4\\ P(B')=1/5\\ P(A'\cup B')=2/5} \Rightarrow \cases{P(A)=1-1/4=3/4\\ P(B)=1-1/5= 4/5\\ P(A\cap B)= 1-2/5= 3/5} \\\Rightarrow P(A\cup B)= P(A)+ P(B)-P(A\cap B) ={3\over 4}+ {4\over 5}-{3\over 5}={19\over 20}，故選\bbox[red,2pt]{(A)}$$
解答：$$出現正正的機率為1/4，骰子出現任何點數的機率皆為1/6，\\\qquad因此其期望值=(1/4)×(1/6)×(2+4+8+10+12)=42/24=7/4\\出現一正一反的機率為1/2，骰子出現任何點數的機率皆為1/6，\\\qquad因此其期望值=(1/2)×(1/6)×(1+2+3+4+5+6)=21/12=7/4\\ 以上兩者相加，即{7\over 4}+{7\over 4}= {7\over 2}，故選\bbox[red,2pt]{(D)}$$
解答：$$2\cos { 1° } \cos { 2° } \times 2\sin { 1° } \csc { 4° } =\frac { 2\cos { 2° } \times \left( 2\sin { 1° } \cos { 1° } \right) }{ \sin { 4° } } \\ =\frac { 2\cos { 2° } \times \sin { 2° } }{ \sin { 4° } } =\frac { \sin { 4° } }{ \sin { 4° } } =1，故選\bbox[red,2pt]{(A)}$$
解答：$${ c }^{ 2 }={ a }^{ 2 }+{ b }^{ 2 }-2ab\cos { \angle C } ={ \left( a-b \right) }^{ 2 }+\left( 2+\sqrt { 3 } \right) ab\\ \Rightarrow -2ab\cos { \angle C } =-2ab+\left( 2+\sqrt { 3 } \right) ab\\ \Rightarrow \cos { \angle C } =\frac { -2ab+\left( 2+\sqrt { 3 } \right) ab }{ -2ab } =\frac { \sqrt { 3 } }{ -2 } \\ \Rightarrow \angle C=150°，故選\bbox[red,2pt]{(C)}$$
解答：$$y=x代入圓C\Rightarrow { \left( x-a \right) }^{ 2 }+{ x }^{ 2 }=1\Rightarrow 2{ x }^{ 2 }-2xa+{ a }^{ 2 }-1=0\Rightarrow 4{ a }^{ 2 }-8\left( { a }^{ 2 }-1 \right) >0\\ \Rightarrow -4{ a }^{ 2 }+8>0\Rightarrow 2>{ a }^{ 2 }\Rightarrow \sqrt { 2 } >a>-\sqrt { 2 }，故選\bbox[red,2pt]{(B)}$$
解答：$${x^2\over 4}-{y^2\over 9}=1之漸近線為{x^2\over 4}={y^2\over 9} \Rightarrow 3x=\pm 2y，故選\bbox[red,2pt]{(B)}$$
======================== END ================================
解題僅供參考，其他
統測試題及詳解
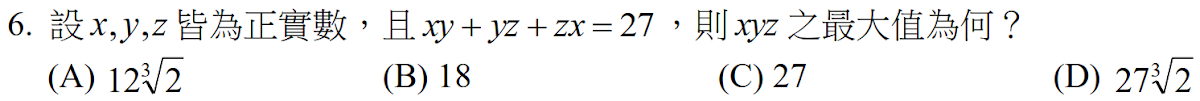
沒有留言:
張貼留言