103 學年度科技校院四年制與專科學校二年制
統一入學測驗 -數學(A)
解答:$$\vec a\cdot \vec b=0 \Rightarrow (1,3)\cdot (2,2-{x\over 3})=2+6-x=0 \Rightarrow x=8,故選\bbox[red,2pt]{(D)}$$
解答:$$\cases{圓心O(1,5)\\ A(x,3)\\ B(4,y)} \Rightarrow O={A+B\over 2} \Rightarrow \cases{1=(x+4)/2\\ 5=(3+y)/2} \Rightarrow \cases{x=-2\\ y=7} \Rightarrow x+y=5,故選\bbox[red,2pt]{(C)}$$
解答:$$本題\bbox[red,2pt]{(送分)}$$
解答:$$假設2x^2+6x+k=0的兩根為\alpha及\beta \Rightarrow \cases{\alpha+\beta =-3\\ \alpha-\beta=1} \Rightarrow \cases{\alpha=-1\\ \beta= -2} \Rightarrow \alpha\beta=2 ={k\over 2} \Rightarrow k=4\\,故選\bbox[red,2pt]{(D)}$$
解答:
$$利用長除法,可得餘式為-9x+5 \Rightarrow \cases{a=-9\\ b=5}\Rightarrow a+b=-4,故選\bbox[red,2pt]{(B)}$$
解答:$$y={1\over 2^{-x+1}} ={1\over 2}\cdot 2^x \Rightarrow \cases{圖形經過(0,1/2)\\ 圖形為遞增} ,故選\bbox[red,2pt]{(A)}$$
解答:
解答:
$$\cases{x+y\ge 2 不含原點\\ 2x+y\le 3包含原點} ,兩圖形如上圖,故選\bbox[red,2pt]{(C)}$$
解答:$$\cases{取到50元硬幣的機率:4/15\\ 取到10元硬幣的機率:5/15\\ 取到5元硬幣的機率:6/15 } \Rightarrow 期望值=50\cdot {4\over 15}+ 10\cdot {5\over 15}+ 5\cdot {6\over 15}= {280\over 15} =18.66\\,故選\bbox[red,2pt]{(A)}$$
解答:$$由題意知:\cases{\mu = 60\\ \sigma=10} \Rightarrow P(X\lt 50 =\mu-\sigma) =P(X\lt \mu-\sigma) =1-(34\%+50\%)=16\%\\ \Rightarrow 1125\times 16\%=180,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{直線的x截距\lt 0\\ 直線的y截距\gt 0} \Rightarrow \cases{-c/a \lt 0\\ -c/b \gt 0} \Rightarrow \cases{ac\gt 0\\ bc\lt 0} \Rightarrow {ac\over bc}={a\over b}\lt 0 \Rightarrow ab\lt 0\\ \Rightarrow \cases{ab \lt 0\\ ac\gt 0} \Rightarrow P(ab,ac)在第二象限,故選\bbox[red,2pt]{(B)}$$
解答:$$\sqrt { 3 } \sin { 480° } +\cos { 300° } +\tan { 225° } \\ =\sqrt { 3 } \sin { \left( 360+120° \right) } +\cos { \left( 360°-60° \right) } +\tan { \left( 180°+45° \right) } \\ =\sqrt { 3 } \sin { 120° } +\cos { \left( -60° \right) } +\tan { 45° } \\ =\sqrt { 3 } \sin { 60° } +\cos { 60° } +\tan { 45° } \\ =\sqrt { 3 } \times \frac { \sqrt { 3 } }{ 2 } +\frac { 1 }{ 2 } +1=3,故選\bbox[red,2pt]{(D)}$$
解答:$$\overrightarrow { a } =\left( x,y \right) =-k\overrightarrow { b } =k(5,-12),其中k\gt 0\\ \Rightarrow \left| \overrightarrow { a } \right| =\sqrt { { k }^{ 2 }\left( { 5 }^{ 2 }+{ \left( -12 \right) }^{ 2 } \right) } =13k=52 \Rightarrow k=4\Rightarrow \overrightarrow { a } =4\left( 5,-12 \right) =\left( 20,-48 \right) \\ \Rightarrow x+y=-28,故選\bbox[red,2pt]{(B)}$$
解答:$$1開頭的數字共有3×2×1=6個,所有的四位數共有4×3×2×1=24個;\\因此大於2000的數字=全部扣去1開頭=24-6=18,故選\bbox[red,2pt]{(C)}$$
解答:$$由題意知:\cases{\mu = 60\\ \sigma=10} \Rightarrow P(X\lt 50 =\mu-\sigma) =P(X\lt \mu-\sigma) =1-(34\%+50\%)=16\%\\ \Rightarrow 1125\times 16\%=180,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{直線的x截距\lt 0\\ 直線的y截距\gt 0} \Rightarrow \cases{-c/a \lt 0\\ -c/b \gt 0} \Rightarrow \cases{ac\gt 0\\ bc\lt 0} \Rightarrow {ac\over bc}={a\over b}\lt 0 \Rightarrow ab\lt 0\\ \Rightarrow \cases{ab \lt 0\\ ac\gt 0} \Rightarrow P(ab,ac)在第二象限,故選\bbox[red,2pt]{(B)}$$
解答:$$\sqrt { 3 } \sin { 480° } +\cos { 300° } +\tan { 225° } \\ =\sqrt { 3 } \sin { \left( 360+120° \right) } +\cos { \left( 360°-60° \right) } +\tan { \left( 180°+45° \right) } \\ =\sqrt { 3 } \sin { 120° } +\cos { \left( -60° \right) } +\tan { 45° } \\ =\sqrt { 3 } \sin { 60° } +\cos { 60° } +\tan { 45° } \\ =\sqrt { 3 } \times \frac { \sqrt { 3 } }{ 2 } +\frac { 1 }{ 2 } +1=3,故選\bbox[red,2pt]{(D)}$$
解答:$$\overrightarrow { a } =\left( x,y \right) =-k\overrightarrow { b } =k(5,-12),其中k\gt 0\\ \Rightarrow \left| \overrightarrow { a } \right| =\sqrt { { k }^{ 2 }\left( { 5 }^{ 2 }+{ \left( -12 \right) }^{ 2 } \right) } =13k=52 \Rightarrow k=4\Rightarrow \overrightarrow { a } =4\left( 5,-12 \right) =\left( 20,-48 \right) \\ \Rightarrow x+y=-28,故選\bbox[red,2pt]{(B)}$$
解答:$$1開頭的數字共有3×2×1=6個,所有的四位數共有4×3×2×1=24個;\\因此大於2000的數字=全部扣去1開頭=24-6=18,故選\bbox[red,2pt]{(C)}$$
解答:$$原來的平均數=(75+65+58+80+72)/5 =350/5=70\\ \Rightarrow 新的平均數=70\times {4\over 5}+9=65,故選\bbox[red,2pt]{(A)}$$
解答:$$(A)\times:\cases{a=1\\ b=-3} \Rightarrow a\gt b,但\cases{|a|=1\\ |b|=3} \Rightarrow |a|\lt |b|\\(B)\times: \cases{a=2\\ b=1\\ c=-1\\ d=-2}滿足a\gt b且c\gt d,但ac=bd=-2 \\(C)\times:\cases{a=2\\ b=-1}滿足a\gt b,但{1\over a}\not \lt {1\over b}\\,故選\bbox[red,2pt]{(D)}$$
解答:
解答:$$(A)\times:\cases{a=1\\ b=-3} \Rightarrow a\gt b,但\cases{|a|=1\\ |b|=3} \Rightarrow |a|\lt |b|\\(B)\times: \cases{a=2\\ b=1\\ c=-1\\ d=-2}滿足a\gt b且c\gt d,但ac=bd=-2 \\(C)\times:\cases{a=2\\ b=-1}滿足a\gt b,但{1\over a}\not \lt {1\over b}\\,故選\bbox[red,2pt]{(D)}$$
解答:
$$|x|+|y|\le 1所圍區域(見上圖)頂點坐標\cases{A(-1,0)\\ B(0,1)\\ C(1,0)\\ D(0,-1)} \Rightarrow \cases{f(A)=-2\\ f(B)=-3\\ f(C)= 2\\ f(D)=3} \Rightarrow 最大值為3,故選\bbox[red,2pt]{(D)}$$
解答:$$令公差為k,則19=-5+6k \Rightarrow k=4 \Rightarrow a+b+c+d +e =-5\times 5+(k+2k+3k +4k+5k) \\ =-25+15k= -25+15\times 4=35,故選\bbox[red,2pt]{(A)}$$
解答:$$\cases{黑桃2-10點有9張\\ 紅心2-10點有9張} \Rightarrow 所求機率 ={C^9_1C^9_1\over C^{52}_2} ={81\over 1326} ={27\over 442},故選\bbox[red,2pt]{(B)}$$
解答:$$\left( \log _{ 2 }{ 27 } -\log _{ 4 }{ 9 } \right) \left( \log _{ 3 }{ 16 } -\log _{ \frac { 1 }{ 3 } }{ 2 } \right) =\left( \frac { 3\log { 3 } }{ \log { 2 } } -\frac { 2\log { 3 } }{ 2\log { 2 } } \right) \left( \frac { 4\log { 2 } }{ \log { 3 } } -\frac { \log { 2 } }{ -\log { 3 } } \right) \\ =\frac { 2\log { 3 } }{ \log { 2 } } \times \frac { 5\log { 2 } }{ \log { 3 } } =10,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{團隊中沒有護士有C^5_5=1種選法\\ 團隊中只有一名護士有C^5_4C^3_1=15種選法\\ 8人任選5人有C^8_5=56種選法} \Rightarrow 至少有2位護士的選法=56-1-15=40\\,故選\bbox[red,2pt]{(A)}$$
解答:$$f(x)=103x^3+ ax^2+bx =(x^2-1)p(x)+3x+4 \Rightarrow \cases{f(1)=103+a+b=7\\ f(-1)=-103+a-b=1} \\ \Rightarrow \cases{a+b=-96\\ a-b=104} \Rightarrow \cases{a=4\\ b=-100} \Rightarrow f(x)=103x^3+4x^2-100x =103(x^3-x)+4x^2+3x \\ \Rightarrow 4x^2+3x= cx^2+dx+e \Rightarrow c=4,故選\bbox[red,2pt]{(B)}$$
解答:$$餘弦定理:{ a }^{ 2 }={ 5 }^{ 2 }+{ b }^{ 2 }-2\times 5\times b\times \cos { 60° } \Rightarrow { \left( 7-b \right) }^{ 2 }={ 5 }^{ 2 }+{ b }^{ 2 }-2\times 5\times b\times \cos { 60° } \\ \Rightarrow 49-14b+{ b }^{ 2 }=25+{ b }^{ 2 }-5b \Rightarrow 9b=24\Rightarrow b=\frac { 24 }{ 9 } \\ \Rightarrow a=7-b=7-\frac { 24 }{ 9 } =\frac { 13 }{ 3 },故選\bbox[red,2pt]{(D)}$$
解答:
解答:$$\cases{黑桃2-10點有9張\\ 紅心2-10點有9張} \Rightarrow 所求機率 ={C^9_1C^9_1\over C^{52}_2} ={81\over 1326} ={27\over 442},故選\bbox[red,2pt]{(B)}$$
解答:$$\left( \log _{ 2 }{ 27 } -\log _{ 4 }{ 9 } \right) \left( \log _{ 3 }{ 16 } -\log _{ \frac { 1 }{ 3 } }{ 2 } \right) =\left( \frac { 3\log { 3 } }{ \log { 2 } } -\frac { 2\log { 3 } }{ 2\log { 2 } } \right) \left( \frac { 4\log { 2 } }{ \log { 3 } } -\frac { \log { 2 } }{ -\log { 3 } } \right) \\ =\frac { 2\log { 3 } }{ \log { 2 } } \times \frac { 5\log { 2 } }{ \log { 3 } } =10,故選\bbox[red,2pt]{(B)}$$
解答:$$\cases{團隊中沒有護士有C^5_5=1種選法\\ 團隊中只有一名護士有C^5_4C^3_1=15種選法\\ 8人任選5人有C^8_5=56種選法} \Rightarrow 至少有2位護士的選法=56-1-15=40\\,故選\bbox[red,2pt]{(A)}$$
解答:$$f(x)=103x^3+ ax^2+bx =(x^2-1)p(x)+3x+4 \Rightarrow \cases{f(1)=103+a+b=7\\ f(-1)=-103+a-b=1} \\ \Rightarrow \cases{a+b=-96\\ a-b=104} \Rightarrow \cases{a=4\\ b=-100} \Rightarrow f(x)=103x^3+4x^2-100x =103(x^3-x)+4x^2+3x \\ \Rightarrow 4x^2+3x= cx^2+dx+e \Rightarrow c=4,故選\bbox[red,2pt]{(B)}$$
解答:$$餘弦定理:{ a }^{ 2 }={ 5 }^{ 2 }+{ b }^{ 2 }-2\times 5\times b\times \cos { 60° } \Rightarrow { \left( 7-b \right) }^{ 2 }={ 5 }^{ 2 }+{ b }^{ 2 }-2\times 5\times b\times \cos { 60° } \\ \Rightarrow 49-14b+{ b }^{ 2 }=25+{ b }^{ 2 }-5b \Rightarrow 9b=24\Rightarrow b=\frac { 24 }{ 9 } \\ \Rightarrow a=7-b=7-\frac { 24 }{ 9 } =\frac { 13 }{ 3 },故選\bbox[red,2pt]{(D)}$$
解答:
$$令R為切點(見上圖),則{ \overline { PQ } }^{ 2 }={ \overline { PR } }^{ 2 }+{ \overline { RQ } }^{ 2 }\Rightarrow \left[ { 6 }^{ 2 }+{ 8 }^{ 2 } \right] ={ 2 }^{ 2 }+{ \overline { RQ } }^{ 2 }\\ \Rightarrow { \overline { RQ } }^{ 2 }=96\Rightarrow \overline { RQ } =\sqrt { 96 } =4\sqrt { 6 } \Rightarrow \triangle PQR=\overline { PR } \times \overline { RQ } \div 2=2\times 4\sqrt { 6 } \div 2=4\sqrt { 6 }\\,故選\bbox[red,2pt]{(C)}$$
解答:$$f\left( x \right) =\cos ^{ 2 }{ x } -2\sin { x } +5=\left( 1-\sin ^{ 2 }{ x } \right) -2\sin { x } +5 =-{ \left( \sin { x } +1 \right) }^{ 2 }+7\\ 當\sin x=1時,f(x)=-4+7=3為最小值,故選\bbox[red,2pt]{(C)}$$
======================== END ================================
解題僅供參考,其他統測試題及詳解
======================== END ================================
解題僅供參考,其他統測試題及詳解

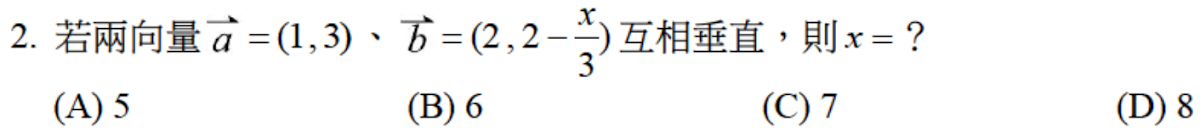



























請問一下19題分子為什麼不是c(2,1)*c(9,1)*c(1,1)*c(9,1)或是考慮紅心黑桃或黑桃紅心所以是9*9*2,因為第一張花色可以是紅心或黑桃,第2張就是另一個花色
回覆刪除你的作法有排列問題,即先紅心或先黑桃;可是題意只要一張黑桃及一張紅心,沒有先後問題。
刪除感謝
刪除