101年大學學測數學科詳解

101 學年度學科能力測驗試題
數學考科詳解

第壹部分：選擇題(占65分)
一、單選題(占35分)

解： $$\sqrt{{1\over 5^2} +{1\over 4^2} +1} =\sqrt{16+25+16\times 25\over 5^2\times 4^2} ={\sqrt{441}\over 5\times 4 } ={21\over 20}={105 \over 100}=1.05，故選\bbox[ red,2pt]{(2)}$$

---

解： $$\begin{cases} 正面=1+2+\cdots+10=55 \\ 左側=1+1+\cdots+1=10\\ 底面=10 \end{cases}\Rightarrow 2(正面+左側+底面)=2(55+10+10) =150，故選\bbox[red,2pt]{(5)}$$

---

解：

$$a=10^{3.032} \Rightarrow \log{a}=3.032\log{10}=3.032 =10 \times 0.3032=10\times\log{2.01} =\log{2.01^{10}}\\ \Rightarrow  a=2.01^{10} \approx 2^{10}=1024，故選\bbox[red,2pt]{(4)}$$

---

解：

$$\begin{array}{cll} (1) &\bigcirc: &符合條件\\ (2)&\times: &學生數相等，所圍面積應相等\\ (3)&\times: &學生數相等，所圍面積應相等\\ (4)&\times: &甲校標準差較大，乙校圖形應較集中(尖)\\ (5)&\times: &甲校標準差較大，乙校圖形應較集中(尖)\\ \end{array}，故選\bbox[red,2pt]{(1)}$$

---

解：
$$\begin{cases} \log_{10}{x}=2.8 \\ \log_{10}{y}=5.6\end{cases} \Rightarrow \begin{cases} x=10^{2.8} \\ y=10^{5.6} \end{cases} \Rightarrow x^2=y \Rightarrow \log_{10}{(x^2+y)} =\log_{10}{(y+y)} =\log_{10}{(2y)} \\ =\log_{10}{2}+\log_{10}{y} =0.301+5.6=5.901，故選\bbox[red,2pt]{(3)}$$

---

解：

$$\begin{array}{c|c|c} |a-b| & (a,b) 或(b,a) & 個數\\\hline 0 & (0,0)-(9,9) &10\\\hline 1 & (0,1),(1,2),\dots,(8,9) & 18\\\hline 4 & (0,4),(1,5),\dots,(5,9) & 12\\\hline 5 & (0,5),(1,6),\dots,(4,9) & 10\\\hline 9 & (0,9) & 2 \end{array}，故選\bbox[red,2pt]{(2)}$$

---

解：

平面$3x+4y=0$包含z軸，球與此平面(看成一面牆)僅交於原點，因此球與坐標軸交於原點及X軸、Y軸各一點，所以共三個交點，故選$\bbox[red,2pt]{(3)}$

---

二、多選題(占30分)

解：

$$f(i)=0 \Rightarrow \pm i \;為\;f(x)=0的根 \Rightarrow x^2+1為f(x)的因式\\ \Rightarrow 利用長除法 f(x)=x^4-5x^3+x^2+ax+b= (x^2-5x)(x^2+1)+(a+5)x+b \\ \Rightarrow 餘式 (a+5)x+b=0 \Rightarrow f(x)=(x^2+1)(x^2-5x)=x(x-5)(x^2+1)\\ \Rightarrow f(x)=0的根為\pm i, 0, 5，故選\bbox[red,2pt]{(1, 2, 5)}$$

---

解：

$$每個邊有2種選擇，共有三個邊，共有2^3=8種三角形；\\其中有兩個是正三角形，見上圖；另六個均為直角三角形，見下圖；\\由餘弦定理可知\cos{60^o}={2^2+1^2-\overline{AC}^2 \over 2\times 2\times 1} \Rightarrow \overline{AC}=\sqrt{3}\\ \Rightarrow \cos{\angle CAB} = {(\sqrt{3})^2 +1^2-2^2 \over 2\times\sqrt{3}\times 1}=0 \Rightarrow \angle CAB=90^o$$

故選$\bbox[red,2pt]{(1,2)}$

---

解：

$$e^{i\theta}=\cos{\theta}+i\sin{\theta} \Rightarrow \begin{cases} z=r_1e^{i\theta_1}\\ w=r_2e^{i\theta_2} \end{cases},其中r_1,r_2\in R且|\theta_1-\theta_2|={\pi\over 2}\\ (1)\times: {z\over w} = {r_1e^{i\theta_1}\over r_2e^{i\theta_2}} = {r_1\over r_2}e^{i(\theta_1-\theta_2)} = {r_1\over r_2}e^{i(\pm{\pi\over 2})} = {r_1\over r_2}\times \pm i\notin R\\ (2)\times: zw=r_1r_2e^{i(\theta_1+\theta_2)}不一定是實數\\ (3)\times:(zw)^2=\left( r_1r_2e^{i(\theta_1+\theta_2)}\right)^2 =r_1^2r_2^2e^{i2(\theta_1+\theta_2)}不一定是實數\\ (4)\bigcirc:{z^2\over w^2}= {{r_1^2e^{i2\theta_1}} \over {r_2^2e^{i2\theta_2}}} ={r_1^2\over r_2^2}e^{i2(\theta_1-\theta_2)} ={r_1^2\over r_2^2}e^{\pm i\pi} ={r_1^2\over r_2^2}\times (-1)為負實數 \\(5)\bigcirc:(z\bar{w})^2=\left( r_1e^{ i\theta_1} r_2e^{-i\theta_2}\right)^2 =r_1^2e^{i2\theta_1}r_2^2e^{-i2\theta_2} =r_1^2r_2^2e^{i2(\theta_1-\theta_2)} =r_1^2r_2^2e^{\pm i\pi} =r_1^2r_2^2\times(-1)為負實數\\ 故選\bbox[red, 2pt]{(4,5)}$$

---

解：

$$\begin{cases} \begin{cases} ax+8y=c\\ x-4y=3 \end{cases}有解 \Rightarrow \begin{cases} 有1組解 \Rightarrow {a\over 1}\ne {8 \over -4} \Rightarrow a\ne -2\\ 有無限多組解 \Rightarrow {a\over 1}= {8 \over -4}= {c\over 3} \Rightarrow \begin{cases} a=-2 \\c=-6\end{cases} \end{cases} \\ \begin{cases} -3x+by=d\\ x-4y=3 \end{cases} 無解 \Rightarrow {-3\over 1} = {b\over -4}\ne {d\over 3} \Rightarrow \begin{cases} b=12\\ d\ne -9 \end{cases}\end{cases}\\ \Rightarrow (a,b,c,d)=(-2, 12, -6, d\ne -9),(a\ne -2,12,c, d\ne -9)\\ (1)\times: a可以是-2,也可以不是-2\\ (2)\times:c可以是-6,也可以不是-6\\ (3)\bigcirc:b一定是12\\ (4)\bigcirc:d一定不是-9\\(5)\times:\begin{cases} ax+8y=c\\ -3x+by=d \end{cases}無解 \Rightarrow {a\over -3} = {8\over b=12} ={2\over 3}\ne {c\over d}不一定成立(a可能不是-2)\\ ，故選：\bbox[red,2pt]{(3,4)}$$

---

解：
$$\tan{\theta}={2\over 3} \Rightarrow P在直線y={2\over 3}x上，又P之y坐標為-4 \Rightarrow P=(-6,-4)\\ (1)\times:x=-6\\ (2)\bigcirc:\overline{OP}=\sqrt{(-6)^2+(-4)^2} =\sqrt{52}= 2\sqrt{13}\\ (3)\times:P在第3象限\Rightarrow \cos{\theta}<0 \\(4)\bigcirc:P在第3象限\Rightarrow \begin{cases} \sin{\theta}<0\\\cos{\theta}<0 \end{cases} \Rightarrow \sin{2\theta} =2\sin{\theta}\cos{\theta} >0 \\(5)\times:\cos{\theta}<0 \Rightarrow 2\cos^2{\theta \over 2}-1<0 \Rightarrow \cos^2{\theta \over 2}<{1\over 2} \Rightarrow -{\sqrt{2}\over 2}<\cos{\theta \over 2}<{\sqrt{2}\over 2}\\故選\bbox[red, 2pt]{(2,4)}$$

---

解：

$$(1)\bigcirc:d=0時，\Gamma為\overline{F_1F_2}的中垂線\\ (2)\bigcirc:合乎雙曲線的定義\\ (3)\times:d=2\Rightarrow \begin{cases} a=1\\c=2 \\b=\sqrt{3} \end{cases} \Rightarrow 圓半徑r=6>c+2a=4\Rightarrow \Gamma之兩頂點皆在圓內\Rightarrow 圓與\Gamma 交四點\\(4)\times:d=4\Rightarrow a=c=2 \Rightarrow \Gamma為兩射線，與圓交兩點 \\(5)\bigcirc:d=8 \Rightarrow \begin{cases}a=4 \\ c=2\end{cases} \Rightarrow a>c \Rightarrow \Gamma不存在\\故選\bbox[red, 2pt]{(1,2,5)}$$

---

第貳部分：選填題(占35分)

解：

$$\begin{cases} a_1=a\\ r=0.01 \end{cases} \Rightarrow S={a_1\over 1-r} \Rightarrow {a\over 1-0.01}=1.\bar{2} =1{2\over 9}= {11\over 9}\\ \Rightarrow a=0.99 \times {11\over 9} =0.11\times 11=\bbox[red,2pt]{1.21}$$

---

解：

斜率要最小，需取左上右下的直線，故取$\overline{CF}$，其斜率為${-6-3\over 8-5} ={-9\over 3} =\bbox[red, 2pt]{-3}$

---

解： $$\begin{cases} 天璇A=(9,8) \\ 天樞B=(7,11) \\ 北極星C=(x,y) \\ \overline{BC}=5\overline{AB}\end{cases} \Rightarrow \begin{cases} {5\times 9+x \over 5+1}=7 \\ {5\times 8+y \over 5+1}=11\end{cases} \Rightarrow \begin{cases} x=-3 \\ y=26 \end{cases} \Rightarrow \bbox[red, 2pt]{(-3,26)}$$

---

解： $$C=(x,{1\over 2}x^2) \Rightarrow \begin{cases} \overrightarrow{AB}=(6,6) \\ \overrightarrow{AC}=(x+2,{1\over 2}x^2-2) \end{cases} \Rightarrow \overrightarrow{AB} \cdot \overrightarrow{AC} =6x+12+3x^2-12=3x^2+6x \\=3(x^2+2x+1)-3 =3(x+1)^2-3 \Rightarrow x=\bbox[red, 2pt]{-1}時，\overrightarrow{AB} \cdot \overrightarrow{AC}有最小值\bbox[red, 2pt]{-3}$$

---

解：

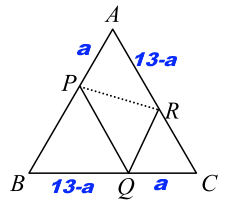
$$\overline{QR}// \overline{AB} \Rightarrow \angle RQC=\angle B=60^o \Rightarrow \triangle RQC為正\triangle ，同理\triangle PBQ也是正\triangle \\ 令\overline{QC}=a =\overline{RQ} =\overline{AP} \Rightarrow \overline{BQ}=13-a =\overline{PQ}= \overline{AR}\\ \Rightarrow {\triangle APR\over \triangle ABC} = {\overline{AP}\times\overline{AR} \over \overline{AB}\times \overline{AC}} \Rightarrow {a(13-a)\over 13^2} ={10\sqrt{3} \over {13^2\sqrt{3} \over 4}} \Rightarrow a(13-a)=40 \Rightarrow a=5, 8\\ 餘弦定理\Rightarrow \cos{\angle A}= {\overline{AP}^2+\overline{AR}^2-\overline{PR}^2 \over 2\overline{AP}\times \overline{AR}} \Rightarrow {1\over 2}= {{64+25-\overline{PR}^2} \over 80} \Rightarrow \overline{PR}=\bbox[red, 2pt]{7}$$

---

解：

$$正\triangle PF_1F_2 \Rightarrow \overline{PF_1} =\overline{PF_2} =\overline{F_1F_2}= 4\Rightarrow \overline{PF_1}+ \overline{PF_2}=2a \Rightarrow 4+4=2a \Rightarrow a=4\\ 又c=\overline{F_1F_2}\div 2=4\div 2=2 \Rightarrow a^2=b^2+c^2 \Rightarrow 4^2=b^2+2^2 \Rightarrow b=2\sqrt{3}\\ \Rightarrow 橢圓方程式為{x^2\over b^2} +{y^2\over a^2}=1\Rightarrow {x^2\over 12}+ {y^2\over 16}=1 \Rightarrow \bbox[red, 2pt] {\begin{cases} m=12\\ n=16\end{cases} }$$

---

解：

由題意可知該長方體各邊長度分別1、2、3，如上圖；
任二頂點可得一條直線，共有$C^8_2=28$直線；對任一頂點而言，只有三條直線長度超過3，如上圖的綠色直線，因此共有$3\times 4=12$直線長度超過3，機率為${12\over 28}= \bbox[red, 2pt]{3\over 7}$。

---

-- END --