90學年四技二專統測--數學(A)詳解

試題來源：技專校院入學測驗中心

解：

利用長除法可得 a=1,b=-1,c=3,d=-2, e=-4, 因此a+b+c+d+e=1-1+3-2-4=-3，故選$\bbox[red,2pt]{(D)}$。

---

解： $$4x^{ 2 }-4x-1=0\Rightarrow x(較大根)=\frac { 4+\sqrt { 16+16 }  }{ 8 } =\frac { 4+4\sqrt { 2 }  }{ 8 } =\frac { 1+\sqrt { 2 }  }{ 2 } \\ =0.5+\frac { 1.414 }{ 2 } =0.5+0.707=1.207，故選\bbox[red,2pt]{(B)}。$$

---

解： $$\begin{cases} \overline { AB } =5-2=3 \\ \overline { BC } =\sqrt { 9+1 } =\sqrt { 10 }  \\ \overline { AC } =\sqrt { 9+16 } =5 \end{cases}\Rightarrow \overline { AB } +\overline { BC } +\overline { AC } =8+\sqrt { 10 } ，故選\bbox[red,2pt]{(C)}。$$

---

解： $${ 2 }^{ { x }^{ 2 } }\cdot { 4 }^{ x }\cdot 16={ 8 }^{ x }\cdot 64\Rightarrow { 2 }^{ { x }^{ 2 } }\cdot { \left( { 2 }^{ 2 } \right)  }^{ x }\cdot { 2 }^{ 4 }={ \left( { 2 }^{ 3 } \right)  }^{ x }\cdot { 2 }^{ 6 }\Rightarrow { 2 }^{ x^{ 2 }+2x+4 }=2^{ 3x+6 }\\ \Rightarrow x^{ 2 }+2x+4=3x+6\Rightarrow x^{ 2 }-x-2=0\Rightarrow \left( x-2 \right) \left( x+1 \right) =0\\ \Rightarrow x=2,-1\Rightarrow 2-1=1，故選\bbox[red,2pt]{(A)}。$$

---

解： $$\frac { \log _{ 8 }{ 3 } +\log _{ 8 }{ 9 }  }{ \log _{ 2 }{ 3 } +\log _{ 4 }{ 9 }  } =\frac { \frac { 1 }{ 3 } \log _{ 2 }{ 3 } +\frac { 2 }{ 3 } \log _{ 2 }{ 3 }  }{ \log _{ 2 }{ 3 } +\log _{ 2 }{ 3 }  } =\frac { 1 }{ 2 } ，故選\bbox[red,2pt]{(A)}。$$

---

解： $$\cot{\theta}=3>0,  且P座標y值為負，所以P在第三象限，因此\cos{\theta}=\frac{-3}{\sqrt{10}}\\，故選\bbox[red,2pt]{(A)}。$$

---

解： $${\left(\sin{75^\circ}-\cos{75^\circ}\right)}^2=1-2\sin{75^\circ}\cos{75^\circ}=1-\sin{150^\circ}=1-\frac{1}{2}=\frac{1}{2}\\，故選\bbox[red,2pt]{(D)}。$$

---

解： $$\cos { 2\theta  } =\frac { \sqrt { 3 }  }{ 2 } \Rightarrow 1-2\sin ^{ 2 }{ \theta  } =\frac { \sqrt { 3 }  }{ 2 } \Rightarrow \sin { \theta  } =\sqrt { \frac { 1-\frac { \sqrt { 3 }  }{ 2 }  }{ 2 }  } \\ =\sqrt { \frac { 2-\sqrt { 3 }  }{ 4 }  } =\sqrt { \frac { 8-4\sqrt { 3 }  }{ 16 }  } =\sqrt { \frac { { \left( \sqrt { 6 } -\sqrt { 2 }  \right)  }^{ 2 } }{ 16 }  } =\frac { \sqrt { 6 } -\sqrt { 2 }  }{ 4 } \\，故選\bbox[red,2pt]{(D)}。$$

---

解：假設該方程式為x-2y+k=0，(-3,1)代入可得-3-2+k=0,  所以k=5，故選$\bbox[red,2pt]{(C)}$。

---

解：此題相當於求A至直線的距離，即$\frac{13}{\sqrt{2^2+3^2}}=\sqrt{13}$，故選$\bbox[red,2pt]{(C)}$。

---

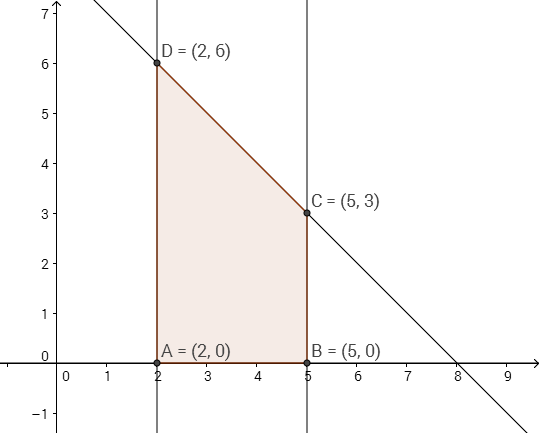
解：

D(2,6)代入有最小值4-6+3=1，故選$\bbox[red,2pt]{(D)}$。

---

解： $$x^{ 2 }+y^{ 2 }+2x-4y-20=0\Rightarrow { \left( x+1 \right)  }^{ 2 }+{ \left( y-2 \right)  }^{ 2 }={ 5 }^{ 2 }\Rightarrow 圓心O(-1,2),半徑r=5,切點P(3,5)\\ \overline { OP } 斜率=\frac { 5-2 }{ 3+1 } =\frac { 3 }{ 4 } \Rightarrow 切線斜率=\frac { -4 }{ 3 } \Rightarrow 切線方程式4x+3y=k\\ P代入切線可得12+15=k\Rightarrow 切線方程式4x+3y=27，故選\bbox[red,2pt]{(A)}。$$

---

解：

$$\overline { AB } =h\sec { \angle A } +h\sec { \angle B } \Rightarrow h=\frac { 80 }{ \sec { \angle A } +\sec { \angle B }  } =\frac { 80 }{ \frac { 1 }{ \sqrt { 3 }  } +\frac { \sqrt { 6 } -\sqrt { 2 }  }{ \sqrt { 6 } +\sqrt { 2 }  }  } =\overline { BC } \sin { \angle B } \\ \Rightarrow \overline { BC } =\frac { 80 }{ \frac { 1 }{ \sqrt { 3 }  } +\frac { \sqrt { 6 } -\sqrt { 2 }  }{ \sqrt { 6 } +\sqrt { 2 }  }  } \times \frac { 4 }{ \sqrt { 6 } +\sqrt { 2 }  } =\frac { 320 }{ \frac { \sqrt { 6 } +\sqrt { 2 }  }{ \sqrt { 3 }  } +\sqrt { 6 } -\sqrt { 2 }  } \\ =\frac { 320\sqrt { 3 }  }{ \sqrt { 6 } +\sqrt { 2 } +\sqrt { 18 } -\sqrt { 6 }  } =\frac { 80\sqrt { 3 }  }{ \sqrt { 2 }  } =40\sqrt { 6 } ，故選\bbox[red,2pt]{(D)}。$$

---

解： $$令A=(0,0),則B=(-3,4),C=(4,3)\Rightarrow \overline { AB } =\overline { AC } =5,\overline { BC } =5\sqrt { 2 } \\ \Rightarrow \overline { AB } +\overline { AC } +\overline { BC } =10+5\sqrt { 2 } ，故選\bbox[red,2pt]{(C)}。$$

---

解： $$\overrightarrow { A } \cdot \overrightarrow { B } =\left| \overrightarrow { A }  \right| \left| \overrightarrow { B }  \right| \cos { \theta  } \Rightarrow 30-4=\sqrt { 36+16 } \times \sqrt { 25+1 } \cos { \theta  } \\ \Rightarrow 26=26\sqrt { 2 } \cos { \theta  } \Rightarrow \cos { \theta  } =\frac { 1 }{ \sqrt { 2 }  } \Rightarrow \theta =45°，故選\bbox[red,2pt]{(B)}。$$

---

解： $${ \left( \frac { 1+i }{ 1-\sqrt { 3 } i }  \right)  }^{ 12 }={ \left[ { \left( \frac { 1+i }{ 1-\sqrt { 3 } i }  \right)  }^{ 2 } \right]  }^{ 6 }={ \left( \frac { -i }{ 1+\sqrt { 3 } i }  \right)  }^{ 6 }={ \left( \frac { 1 }{ 2 } \times \frac { 1 }{ 1+\sqrt { 3 } i }  \right)  }^{ 3 }\\ =\frac { 1 }{ 8 } \left( \frac { 1 }{ -2\left( 1-\sqrt { 3 } i \right)  }  \right) \left( \frac { 1 }{ 1+\sqrt { 3 } i }  \right) =\frac { 1 }{ -16 } \times \frac { 1 }{ 1+3 } =-\frac { 1 }{ 64 } ，故選\bbox[red,2pt]{(A)}。$$

---

解： $$\omega 為x^{ 2 }+x+1=0之一根，即\omega ^{ 2 }+\omega +1=0\Rightarrow \left( \omega -1 \right) \left( \omega ^{ 2 }+\omega +1 \right) =0\Rightarrow \omega ^{ 3 }=1\\ 1+\omega +\omega ^{ 2 }+\cdots +\omega ^{ 10 }=1+\omega +\omega ^{ 2 }+\omega ^{ 3 }\left( 1+\omega +\omega ^{ 2 } \right) +\omega ^{ 6 }\left( 1+\omega +\omega ^{ 2 } \right) +\omega ^{ 9 }+\omega ^{ 10 }\\ =\omega ^{ 9 }+\omega ^{ 10 }=1+\omega =1+\frac { -1+\sqrt { 3 } i }{ 2 } =\frac { 1+\sqrt { 3 } i }{ 2 } ，故選\bbox[red,2pt]{(B)}。$$

---

解： $$\log _{ 3 }{ \left( x+1 \right)  } +\log _{ 3 }{ \left( x-7 \right)  } =\log _{ 3 }{ 20 } \Rightarrow \log _{ 3 }{ \left( x+1 \right) \left( x-7 \right)  } =\log _{ 3 }{ 20 } \\ \Rightarrow \left( x+1 \right) \left( x-7 \right) =20\Rightarrow x^{ 2 }-6x-27=0\Rightarrow \left( x-9 \right) \left( x+3 \right) =0\\\Rightarrow x=9，故選\bbox[red,2pt]{(C)}。$$

---

解： $$x=3代入\Rightarrow  y^2-12-2y+9=0\Rightarrow  (y-3)(y+1)=0\Rightarrow  y=3,y=-1\\\Rightarrow  \overline{AB}=3-(-1)=4，故選\bbox[red,2pt]{(B)}。$$

---

解：中心=(0,0),  c=2,b=4$\Rightarrow  a^2=b^2+c^2=16+4=20$，故選$\bbox[red,2pt]{(B)}$。

---

解： $$f\left( x \right) ={ e }^{ \sin { 2x }  }\Rightarrow f'\left( x \right) ={ 2\cos { 2x } e }^{ \sin { 2x }  }\Rightarrow f'\left( \frac { \pi  }{ 2 }  \right) =-2，故選\bbox[red,2pt]{(A)}。$$

---

解： $$y=\ln { \sqrt { \tan { x } +\sec { x }  }  } \\ \Rightarrow \frac { dy }{ dx } =\frac { 1 }{ \sqrt { \tan { x } +\sec { x }  }  } \times \frac { 1 }{ 2 } \times \frac { 1 }{ \sqrt { \tan { x } +\sec { x }  }  } \times \left( \sec ^{ 2 }{ x } +\sec { x } \tan { x }  \right) \\ =\frac { 1 }{ 2 } \times \frac { \sec { x } \left( \tan { x } +\sec { x }  \right)  }{ \tan { x } +\sec { x }  } =\frac { 1 }{ 2 } \sec { x } ，故選\bbox[red,2pt]{(A)}。$$

---

解： $$V\left( t \right) =t^{ 2 }-\frac { 1 }{ 2 } \sqrt { t } \Rightarrow V'\left( t \right) =2t-\frac { 1 }{ 4 } \frac { 1 }{ \sqrt { t }  } \Rightarrow V'\left( 4 \right) =8-\frac { 1 }{ 8 } =\frac { 63 }{ 8 } \\，故選\bbox[red,2pt]{(C)}。$$

---

解： $$4x^{ 2 }-16y^{ 2 }+4x+16y+1=0\Rightarrow 4(x^{ 2 }+x+\frac { 1 }{ 4 } )-16(y^{ 2 }-y+\frac { 1 }{ 4 } )+4=0\\ \Rightarrow 4{ \left( x+\frac { 1 }{ 2 }  \right)  }^{ 2 }-16{ \left( y-\frac { 1 }{ 2 }  \right)  }^{ 2 }+4=0\Rightarrow \frac { { \left( y-\frac { 1 }{ 2 }  \right)  }^{ 2 } }{ { \left( \frac { 1 }{ 2 }  \right)  }^{ 2 } } -\frac { { \left( x+\frac { 1 }{ 2 }  \right)  }^{ 2 } }{ 1 } =1\\ \Rightarrow 中心\left( -\frac { 1 }{ 2 } ,\frac { 1 }{ 2 }  \right) ,a=\frac { 1 }{ 2 } \Rightarrow 頂點\left( -\frac { 1 }{ 2 } ,\frac { 1 }{ 2 } \pm \frac { 1 }{ 2 }  \right) =\left( -\frac { 1 }{ 2 } ,0 \right) ,\left( -\frac { 1 }{ 2 } ,1 \right) \\，故選\bbox[red,2pt]{(D)}。$$

---

解： $$f\left( x \right) =3x-{ x }^{ 3 }\Rightarrow f'\left( x \right) =3-3{ x }^{ 2 }\Rightarrow f'\left( x \right) =0\Rightarrow 3(x+1)(x-1)=0\Rightarrow x=1,-1\\ \Rightarrow f\left( 1 \right) =3-1=2,f\left( -1 \right) =-3+1=-2\Rightarrow M+m=2-2=0，故選\bbox[red,2pt]{(B)}。$$

---