解：$$\overrightarrow{BC}=\overrightarrow{AD}\Rightarrow (4-0,-8+5)=(x+5,y-4)\\ \Rightarrow (4,-3)=(x+5,y-4)\Rightarrow x=-1,y=1\Rightarrow (x,y)在第二象限，故選\bbox[red,2pt]{(B)}。$$
解：
首數就是取最接近且小於等於\(\log{a}的整數，故選\bbox[red,2pt]{(D)}。\)
解：$$\left( x+2 \right) \left( x+3 \right) \left( x-4 \right) \left( x-5 \right) =60\Rightarrow \left[ \left( x+2 \right) \left( x-4 \right) \right] \left[ \left( x+3 \right) \left( x-5 \right) \right] =60\\ \Rightarrow \left[ { x }^{ 2 }-2x-8 \right] \left[ { x }^{ 2 }-2x-15 \right] =60\Rightarrow { \left( { x }^{ 2 }-2x \right) }^{ 2 }-23\left( { x }^{ 2 }-2x \right) +60=0\\ \Rightarrow \left( { x }^{ 2 }-2x-20 \right) \left( { x }^{ 2 }-2x-3 \right) =0\Rightarrow \left( { x }^{ 2 }-2x-20 \right) \left( x-3 \right) \left( x+1 \right) =0\\，故選\bbox[red,2pt]{(C)}。$$
解：$$f(-3)=20\Rightarrow -9a+2=20 \Rightarrow a=-2，故選\bbox[red,2pt]{(A)}。$$
解：底數需為不為0的正數，因此(B)(C)不合；又對數值需大0，因此(D)也不合，故選\(\bbox[red,2pt]{(A)}。\)
解：$$(A)\cos{\frac{-\pi}{6}}=\cos{\frac{\pi}{6}}；(B)\cos{\frac{2\pi}{6}}=-\cos{\frac{\pi}{6}}\\(C)\sin{\frac{-\pi}{4}}-\sin{\frac{\pi}{4}}，故選\bbox[red,2pt]{(D)}。$$
解：$$\tan{\theta}=\sqrt{2}\Rightarrow \sin{\theta}=\frac{\sqrt{2}}{\sqrt{3}}、\cos{\theta}=\frac{1}{\sqrt{3}}\\ \Rightarrow \sqrt{3}\sin{\theta}+\sqrt{6}\cos{\theta} =\sqrt{2}+\sqrt{2}=2\sqrt{2}，故選\bbox[red,2pt]{(C)}。$$
解：$$令a=\sin { x } +\cos { x } \Rightarrow { a }^{ 2 }=1+2\sin { x } \cos { x } =1+2\sin { 2x } \\ \Rightarrow \sin { 2x } ={ a }^{ 2 }-1\Rightarrow f\left( x \right) =1+\sin { \left( 2x \right) } +4\left( \sin { x } +\cos { x } \right) \\ =1+{ a }^{ 2 }-1+4a={ a }^{ 2 }+4a={ \left( a+2 \right) }^{ 2 }-4\\ a=\sin { x } +\cos { x } \Rightarrow -\sqrt { 2 } \le a\le \sqrt { 2 } \\ \Rightarrow f\left( -\sqrt { 2 } \right) ={ \left( -\sqrt { 2 } +2 \right) }^{ 2 }-4=2-4\sqrt { 2 } 為最小值，故選\bbox[red,2pt]{(C)}。$$
解：$${ \overline { AC } }^{ 2 }={ \overline { AB } }^{ 2 }+{ \overline { BC } }^{ 2 }-2\overline { AB } \times \overline { BC } \times \cos { \angle ABC } \\ ={ 16 }^{ 2 }+{ \left( 15-8\sqrt { 3 } \right) }^{ 2 }-2\times 16\times \left( 15-8\sqrt { 3 } \right) \times \cos { 150° } \\ =256+225-240\sqrt { 3 } +192-\left( 480-256\sqrt { 3 } \right) \left( \frac { -\sqrt { 3 } }{ 2 } \right) \\ =673-240\sqrt { 3 } -\left( 384-240\sqrt { 3 } \right) =289\\ \Rightarrow \overline { AC } =17，故選\bbox[red,2pt]{(B)}。$$
解：$$\overrightarrow { a } \cdot \left( 3\overrightarrow { b } -\overrightarrow { c } \right) =3\overrightarrow { a } \cdot \overrightarrow { b } -\overrightarrow { a } \cdot \overrightarrow { c } =18-\overrightarrow { a } \cdot \overrightarrow { c } =9\Rightarrow \overrightarrow { a } \cdot \overrightarrow { c } =9\\，故選\bbox[red,2pt]{(D)}。$$
解：$$\overrightarrow { u } \cdot \overrightarrow { v } =\left| \overrightarrow { u } \right| \left| \overrightarrow { v } \right| \cos { \theta } \Rightarrow \frac { 1 }{ 2 } =\cos { \theta } \Rightarrow \theta =60^{ \circ }，故選\bbox[red,2pt]{(C)}。$$
解：$${ \left( -i \right) }^{ 8 }+{ \left( -i \right) }^{ 7 }-{ \left( -i \right) }^{ 6 }+{ \left( -i \right) }^{ 5 }+{ \left( -i \right) }^{ 4 }-{ \left( -i \right) }^{ 3 }-{ \left( -i \right) }^{ 2 }+\left( -i \right) +1\\ ={ i }^{ 8 }-{ i }^{ 7 }-{ i }^{ 6 }-{ i }^{ 5 }+{ i }^{ 4 }+{ i }^{ 3 }-{ i }^{ 2 }-i+1=1-{ i }^{ 3 }-{ i }^{ 2 }-{ i }+1+{ i }^{ 3 }-{ i }^{ 2 }-i+1\\ =1+i+1-{ i }+1-i+1-i+1=5-2i，故選\bbox[red,2pt]{(D)}。$$
解：$${ \omega }^{ 2 }+\omega +1=0\Rightarrow { \omega }^{ 3 }+{ \omega }^{ 2 }+\omega =0\Rightarrow { \omega }^{ 3 }=-\left( { \omega }^{ 2 }+\omega +1 \right) +1\Rightarrow { \omega }^{ 3 }=1\\ \Rightarrow \left( 2-\omega \right) \left( 2-{ \omega }^{ 2 } \right) =4-2{ \omega }^{ 2 }-2\omega +{ \omega }^{ 3 }=-2\left( { \omega }^{ 2 }+\omega +1 \right) +6+{ \omega }^{ 3 }\\ =0+6+{ \omega }^{ 3 }=6+1=7，故選\bbox[red,2pt]{(B)}。$$
解：$$\left| \begin{matrix} 1 & 10 & 20 \\ 5 & 50 & 1 \\ 10 & 1 & 5 \end{matrix} \right| =\left| \begin{matrix} 1 & 0 & 20 \\ 5 & 0 & 1 \\ 10 & -99 & 5 \end{matrix} \right| =-9900+99=-9801=-{ 99 }^{ 2 }，故選\bbox[red,2pt]{(A)}。$$
解：
直線通過(0,6)，即b=6；直線通過(3,0)，即0=3a+b=3a+6，因此a=-2；3a+2b=-6+12=6，故選\(\bbox[red,2pt]{(C)}。\)
解：$$\overline{AB}的斜率=\frac{2}{b-a}，垂直平分線斜率=-2\Rightarrow \frac{2}{b-a}\times(-2)=-1\Rightarrow b-a=4\\
A、B中點C坐標=\left(\frac{a+b}{2},\frac{1+3}{2}\right)=\left(\frac{a+b}{2},2\right)\\ C經過垂直平分線\Rightarrow a+b+2=4\Rightarrow a+b=2\\由上兩式知 a=-1,b=3\Rightarrow 2a+b=-2+3=1，故選\bbox[red,2pt]{(A)}。$$
解：$$\frac { { \left( x-1 \right) }^{ 2 }\left( x+3 \right) }{ x-2 } <0\Rightarrow { \left( x-1 \right) }^{ 2 }\left( x+3 \right) \left( x-2 \right) <0\Rightarrow \left( x+3 \right) \left( x-2 \right) <0\\ \Rightarrow -3<x<2\Rightarrow 整數解\quad x=-2,-1,0(x=1不合)，故選\bbox[red,2pt]{(C)}。$$
解：$$c^2=16+9\Rightarrow c=5\Rightarrow 2c=10，故選\bbox[red,2pt]{(C)}。$$
解：$$f\left( x \right) =\left( x-1 \right) \left( x-2 \right) \left( x-3 \right) ={ x }^{ 3 }-6{ x }^{ 2 }+11x-6\\ \Rightarrow f'\left( x \right) =3{ x }^{ 2 }-12x+11\Rightarrow f''\left( x \right) =6x-12\\ f''\left( x \right) =0\Rightarrow x=2，故選\bbox[red,2pt]{(A)}。$$
解：$$f\left( x \right) =\frac { { x }^{ 2 }+300 }{ x+10 } \Rightarrow f'\left( x \right) =\frac { 2x }{ x+10 } -\frac { { x }^{ 2 }+300 }{ { \left( x+10 \right) }^{ 2 } } =\frac { \left( x-10 \right) \left( x+30 \right) }{ { \left( x+10 \right) }^{ 2 } } \\ f'\left( x \right) =0\Rightarrow x=10\left( 0\le x\le 30,x=-30不合 \right) \Rightarrow f\left( 10 \right) =\frac { 400 }{ 20 } =20，故選\bbox[red,2pt]{(D)}。$$
解：$$\int _{ 1 }^{ 4 }{ \left( 2f\left( x \right) +g\left( x \right) \right) } dx=2\left( \int _{ 1 }^{ 2 }{ f\left( x \right) } dx+\int _{ 2 }^{ 4 }{ f\left( x \right) } dx \right) +\int _{ 1 }^{ 2 }{ g\left( x \right) } dx+\int _{ 2 }^{ 4 }{ g\left( x \right) } dx\\ =2\left( 1+3 \right) +2+5=15，故選\bbox[red,2pt]{(B)}。$$
解：$$\int _{ -1 }^{ 1 }{ f\left( x \right) dx } =\left. F\left( x \right) \right| _{ -1 }^{ 1 }\left. =\ln { (x+2) } \right| _{ -1 }^{ 1 }=\ln { 3 } -\ln { 1 } =\ln { 3 } ，故選\bbox[red,2pt]{(A)}。$$
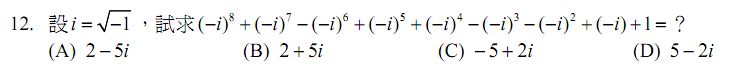
沒有留言:
張貼留言