解：$$\overrightarrow{BC}=\overrightarrow{AD}\Rightarrow (4-0,-8+5)=(x+5,y-4)\\ \Rightarrow (4,-3)=(x+5,y-4)\Rightarrow x=-1,y=1\Rightarrow (x,y)在第二象限，故選\bbox[red,2pt]{(B)}。$$
解：
首數就是取最接近且小於等於\(\log{a}的整數，故選\bbox[red,2pt]{(D)}。\)
解：$$\left( x+2 \right) \left( x+3 \right) \left( x-4 \right) \left( x-5 \right) =60\Rightarrow \left[ \left( x+2 \right) \left( x-4 \right) \right] \left[ \left( x+3 \right) \left( x-5 \right) \right] =60\\ \Rightarrow \left[ { x }^{ 2 }-2x-8 \right] \left[ { x }^{ 2 }-2x-15 \right] =60\Rightarrow { \left( { x }^{ 2 }-2x \right) }^{ 2 }-23\left( { x }^{ 2 }-2x \right) +60=0\\ \Rightarrow \left( { x }^{ 2 }-2x-20 \right) \left( { x }^{ 2 }-2x-3 \right) =0\Rightarrow \left( { x }^{ 2 }-2x-20 \right) \left( x-3 \right) \left( x+1 \right) =0\\，故選\bbox[red,2pt]{(C)}。$$
解：$$f(-3)=20\Rightarrow -9a+2=20 \Rightarrow a=-2，故選\bbox[red,2pt]{(A)}。$$
解：$${ \left( 81 \right) }^{ x }=\frac { \sqrt { 3 } }{ 27 } \Rightarrow { \left( { 3 }^{ 4 } \right) }^{ x }=\frac { { 3 }^{ \frac { 1 }{ 2 } } }{ { 3 }^{ 3 } } \Rightarrow { 3 }^{ 4x }={ 3 }^{ -\frac { 5 }{ 2 } }\Rightarrow 4x=-\frac { 5 }{ 2 } \Rightarrow x=-\frac { 5 }{ 8 } \\，故選\bbox[red,2pt]{(A)}。$$
解：$$\tan { \theta } =\sqrt { 3 } \Rightarrow \sin { \theta } =\frac { \sqrt { 3 } }{ 2 } ,\cos { \theta } =\frac { 1 }{ 2 } \Rightarrow \sin { \theta } \cos { \theta } =\frac { \sqrt { 3 } }{ 2 } \times \frac { 1 }{ 2 } \\=\frac { \sqrt { 3 } }{ 4 } ，故選\bbox[red,2pt]{(C)}。$$
解：$$\begin{cases} { a }_{ 9 }=58 \\ { a }_{ 15 }=100 \end{cases}\Rightarrow \begin{cases} { a }_{ 1 }+8d=58 \\ { a }_{ 1 }+14d=100 \end{cases}\Rightarrow { a }_{ 1 }=2,d=7\\ { a }_{ 1 }+\left( n-1 \right) d=674\Rightarrow 2+7\left( n-1 \right) =674\Rightarrow n=97，故選\bbox[red,2pt]{(D)}。$$
解：$$\sum _{ n=0 }^{ \infty }{ \frac { { 2 }^{ n }+5 }{ { 3 }^{ n } } } =\left[ 1+\frac { 2 }{ 3 } +{ \left( \frac { 2 }{ 3 } \right) }^{ 2 }+\cdots \right] +\left[ 5\left( 1+\frac { 1 }{ 3 } +\frac { 1 }{ { 3 }^{ 2 } } +\cdots \right) \right] \\ =\frac { 1 }{ 1-\frac { 2 }{ 3 } } +5\left( \frac { 1 }{ 1-\frac { 1 }{ 3 } } \right) =3+5\times \frac { 3 }{ 2 } =\frac { 21 }{ 2 } ，故選\bbox[red,2pt]{(C)}。$$
解：$$\frac { 4-2 }{ -5-3 } =\frac { k-2 }{ -3-3 } \Rightarrow \frac { 2 }{ -8 } =\frac { k-2 }{ -6 } \Rightarrow 4\left( k-2 \right) =6\Rightarrow k=3\frac { 1 }{ 2 } \\，故選\bbox[red,2pt]{(B)}。$$
解：
解：
$$\left| x-1 \right| +\left| y-3 \right| =2包含四條直線，即\begin{cases} (x-1)+(y-3)=2 \\ (1-x)+(y-3)=2 \\ (x-1)+(3-y)=2 \\ (1-x)+(3-y)=2 \end{cases}\equiv \begin{cases} x+y=6 \\ -x+y=4 \\ x-y=0 \\ x+y=2 \end{cases}\\ 四直線交點A,B,C,D如上圖\Rightarrow x+2y=1+2\times 5=11為最大值，故選\bbox[red,2pt]{(D)}。$$
解：$$f\left( x \right) =\left| x+4 \right| +\left| x-3 \right| =\begin{cases} 2x+1 & x\ge 3 \\ 7 & -4\le x\le 3 \\ -2x-1 & x\le -4 \end{cases}\\，故選\bbox[red,2pt]{(C)}。$$
解：$$x^2+y^2-6x+4y-12=0\Rightarrow {(x-3)}^2+{(y+2)}^2=5^2\Rightarrow 圓心(3,-2), 半徑5\\點(-1,1)在切線上\Rightarrow 1=-m+b\Rightarrow b=m+1\\圓心至切線距離=半徑\Rightarrow \left|\frac{3m+b+2}{\sqrt{m^2+1}}\right|=\left|\frac{4m+3}{\sqrt{m^2+1}}\right|=5\\ \Rightarrow \frac{{(4m+3)}^2}{m^2+1}=25\Rightarrow {(3m-4)}^2=0\Rightarrow m=\frac{4}{3}\\ \Rightarrow 2m+b=3m+1=4+1=5，故選\bbox[red,2pt]{(B)}。$$
解：$$半徑=\left( 2,-3 \right) 至\left( -1,5 \right) 距離=\sqrt { 3^{ 2 }+8^{ 2 } } =\sqrt { 73 } \\ 圓心\left( 2,-3 \right) 及半徑\sqrt { 73 } \Rightarrow 圓方程式:{ (x-2) }^{ 2 }+{ (y+3) }^{ 2 }=73\\ \Rightarrow x^2-4x+4+y^2+6y+9=73\Rightarrow x^2+y^2-4x+6y-60=0，故選\bbox[red,2pt]{(A)}。$$
解：
不限每輛車的載客限制，有\(3^5=243\)種載客方式，扣除一輛車載五個人的3種情況(5,0,0)、(0,5,0)及(0,0,5)，即共有243-3=240組解，故選\(\bbox[red,2pt]{(C)}。\)
百位數不得為0，有9種情況；十位數只有1種情況；個位數必須是0,2,4,6,8，有5種情況，因此共有\(9\times 1\times 5=45個，故選\bbox[red,2pt]{(C)}。\)
x+y+z=5的正整數解個數，相當於x+y+z=2的非負整數解個數，即\(H_2^3=C_2^4=6，故選\bbox[red,2pt]{(A)}。\)
假設不公正硬幣出現正面的機率為p、出現背面的機率為1-p；公正硬幣出現正面與反面的機率皆為1/2。因此兩枚都出現正面的機率為\(\frac{1}{2}p=\log{3}\Rightarrow p=2\log{3}，
故選\bbox[red,2pt]{(C)}。\)
選到甲袋且取出白球的機率=\(\frac{1}{2}\times\frac{3}{5}\)，選到乙袋且取出白球的機率=\(\frac{1}{2}\times\frac{1}{5}\)，兩者相加=\(\frac{2}{5}，故選\bbox[red,2pt]{(B)}\)。
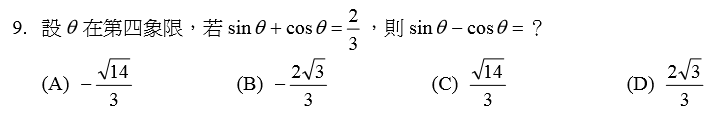
沒有留言:
張貼留言