解:
解:
x=3代入可得27-54+33-6=0,故選\(\bbox[red,2pt]{(D)}\)。
解:$$\sqrt{{(2-1)}^2+{(5-3)}^2}=\sqrt{5},故選\bbox[red,2pt]{(B)}。$$
解:$${\left(\frac{1}{27}\right)}^3\times{81}^2={3}^{-9}\times{3}^{8}=3^{-1}=\frac{1}{3},故選\bbox[red,2pt]{(A)}。$$
解:$$\log _{ 10 }{ 3 } +\log _{ 10 }{ 50 } +\log _{ 10 }{ 7 } -\log _{ 10 }{ 105 } \\ =\log _{ 10 }{ 3 } +1+\log _{ 10 }{ 5 } +\log _{ 10 }{ 7 } -\log _{ 10 }{ 3 } -\log _{ 10 }{ 5 } -\log _{ 10 }{ 7 } \\ =1,故選\bbox[red,2pt]{(A)}。$$
解:$$\sin { 2002° } =\sin { \left( 365°\times 5+202° \right) } =\sin { 202° } =-\sin { 22° } =\frac { -k }{ \sqrt { k^{ 2 }+1 } } \\,故選\bbox[red,2pt]{(D)}。$$
解:$$\overrightarrow { a } \cdot \overrightarrow { b } =\left| \overrightarrow { a } \right| \left| \overrightarrow { b } \right| \cos { \theta } =\sqrt { 13 } \times \sqrt { 13 } \cos { \theta } =13\cos { \theta } ,故選\bbox[red,2pt]{(C)}。$$
解:令圓心坐標(x,y),圓心至三點距離相等,即$$\begin{cases} { \left( x-4 \right) }^{ 2 }+{ y }^{ 2 }={ \left( x+4 \right) }^{ 2 }+{ y }^{ 2 } \\ { \left( x-4 \right) }^{ 2 }+{ y }^{ 2 }=x^{ 2 }+{ \left( y-3 \right) }^{ 2 } \end{cases}\Rightarrow \begin{cases} x=0 \\ 16+{ y }^{ 2 }=y^{ 2 }-6y+9 \end{cases}\Rightarrow \begin{cases} x=0 \\ y=\frac { -7 }{ 6 } \end{cases}\\ 半徑=\sqrt { 16+\frac { 49 }{ 36 } } =\sqrt { \frac { 625 }{ 36 } } =\frac { 25 }{ 6 } ,故選\bbox[red,2pt]{(B)}。$$
解:經過(0,0)及(1,1)的方程式為y=x=f(x);經過(1,1,)及(3,0)的方程式為y=g(x)=\(\frac{3-x}{2}\)。u(x)=f(x)g(x)\(\Rightarrow\)u'(x)=f'(x)g(x)+f(x)g'(x)=\(\frac{3-x}{2}+(\frac{-1}{2})x \Rightarrow\)u'(1)=1+(-0.5)=0.5,故選\(\bbox[red,2pt]{(C)}\)。
解:$$\frac { 1-3i }{ 1+i } =\frac { \left( 1-3i \right) \left( 1-i \right) }{ \left( 1+i \right) \left( 1-i \right) } =\frac { -2-4i }{ 2 } =-1-2i=a+bi\\ \Rightarrow a+b=-1-2=-3,故選\bbox[red,2pt]{(A)}。$$
解:D位於B、C的中點,即D=\(\left(\frac{2-3}{2},\frac{1-1}{2}\right)=\left(\frac{-1}{2},0\right)\)。令經過A、D的直線方程式為y=mx+b,將A、D坐標代入可得m=-6,b=-3,故選\(\bbox[red,2pt]{(D)}\)。
解:$$\int _{ -1 }^{ 1 }{ { (1-x }^{ 2 }) } dx=\left. \left( x-\frac { 1 }{ 3 } { x }^{ 3 } \right) \right| _{ -1 }^{ 1 }=\frac { 2 }{ 3 } +\frac { 2 }{ 3 } =\frac { 4 }{ 3 } ,故選\bbox[red,2pt]{(D)}。$$
解:
(B)\(\cos{0}=1\);(C)\(\sin{2x}=2\sin{x}\cos{x}\);(D)\(\tan{(x+y)}=\frac{\tan{x}+\tan{y}}{1-\tan{x}\tan{y}}\),故選\(\bbox[red,2pt]{(A)}\)。
解:\(\overrightarrow{AB}\)=(3-1,k-3)=(2,k-3); \(\overrightarrow{AC}\)=(5-1,1-3)=(4,-2)。
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=0\Rightarrow8-2k+6=0\Rightarrow k=7\),故選\(\bbox[red,2pt]{(D)}\)。
解:$${ a }^{ 2 }={ b }^{ 2 }+c^{ 2 }-2bc\cos { \angle A } \Rightarrow 12=4+c^{ 2 }-4\times c\times \left( \frac { -1 }{ 2 } \right) \Rightarrow c^{ 2 }+2c-8=0\\ \Rightarrow (c+4)(c-2)=0\Rightarrow c=2,故選\bbox[red,2pt]{(B)}。$$
解:$$\overline { AC } =8,\overline { AB } =\sqrt { { \left( 8-\frac { 11 }{ 2 } \right) }^{ 2 }+{ \left( \frac { 5\sqrt { 3 } }{ 2 } \right) }^{ 2 } } =\sqrt { \frac { 25 }{ 4 } +\frac { 75 }{ 4 } } =\frac { 10 }{ 2 } =5\\ \overline { BC } =\sqrt { { \left( \frac { 11 }{ 2 } \right) }^{ 2 }+{ \left( \frac { 5\sqrt { 3 } }{ 2 } \right) }^{ 2 } } =\sqrt { \frac { 121 }{ 4 } +\frac { 75 }{ 4 } } =\frac { 14 }{ 2 } =7\\ { \overline { BC } }^{ 2 }={ \overline { AB } }^{ 2 }+{ \overline { AC } }^{ 2 }-2\overline { AB } \overline { AC } \cos { \angle BAC } \Rightarrow 49=25+64-80\cos { \angle BAC } \\ \Rightarrow \cos { \angle BAC } =\frac { 1 }{ 2 } \Rightarrow \angle BAC=60°,故選\bbox[red,2pt]{(C)}。$$
解:四頂點分別為A(0,0)、B(a,0)、C(a,b)、D(0,b),且a>0,b>0, a+2b=6
ABCD面積=\(a\times b=(6-2b)b=6b-2b^2=-2(b^2-3b+\frac{9}{4})+\frac{9}{2}=-2{(b-\frac{3}{2})}^2+\frac{9}{2}\)
當\(b=\frac{3}{2}, 面積有最大值\frac{9}{2}\Rightarrow\) 周長=2(a+b)=2(6-b)=12-3=9,故選\(\bbox[red,2pt]{(B)}\)。
解:$$\tan { \theta } =\frac { 3 }{ 4 } \Rightarrow \cos { \theta } =\frac { 4 }{ 5 } \Rightarrow \cos { 2\theta } =2\cos ^{ 2 }{ \theta } -1\\ =2\times \frac { 16 }{ 25 } -1=\frac { 7 }{ 25 } ,故選\bbox[red,2pt]{(A)}。$$
解:$${ \left( \sqrt { 3 } +i \right) }^{ 10 }={ \left[ 2\left( \frac { \sqrt { 3 } }{ 2 } +\frac { 1 }{ 2 } i \right) \right] }^{ 10 }={ \left[ 2\left( \cos { \frac { \pi }{ 6 } } +i\sin { \frac { \pi }{ 6 } } \right) \right] }^{ 10 }\\ ={ 2 }^{ 10 }\left( \cos { \frac { 10\pi }{ 6 } } +i\sin { \frac { 10\pi }{ 6 } } \right) ={ 2 }^{ 10 }\left( \cos { \frac { \pi }{ 3 } } -i\sin { \frac { \pi }{ 3 } } \right) \\ ={ 2 }^{ 10 }\left( \frac { 1 }{ 2 } -\frac { \sqrt { 3 } }{ 2 } i \right) ={ 2 }^{ 9 }\left( 1-\sqrt { 3 } i \right) ,故選\bbox[red,2pt]{(B)}。$$
解:該圖形為橢圓,兩焦點為(1,1), (7,1), 2a=10\(\Rightarrow 中心坐標=(\frac{1+7}{2},\frac{1+1}{2})=(4,1),a=5\),故選\(\bbox[red,2pt]{(C)}\)。
解:$$\int _{ \sqrt { 3 } }^{ \sqrt { 8 } }{ \frac { x }{ \sqrt { { x }^{ 2 }+1 } } dx } =\left. \left( \sqrt { { x }^{ 2 }+1 } \right) \right| _{ \sqrt { 3 } }^{ \sqrt { 8 } }=3-2=1,故選\bbox[red,2pt]{(A)}。$$
解:由拋物線方程式可知c=1, 因此焦點=(1,2+1)=(1,3)。(5,6)至(1,3)距離=\(\sqrt{4^2+3^2}=5\),故選\(\bbox[red,2pt]{(D)}\)。
解:2x-3y+6=0的斜率為\(\frac{2}{3}\Rightarrow\)直線L的斜率為\(\frac{-3}{2}\Rightarrow\) 方程式為\(y=\frac{-3}{2}x+b\)且經過(1,5)\(\Rightarrow 5=\frac{-3}{2}+b\Rightarrow b=\frac{13}{2}\)。因此L: \(y=\frac{-3}{2}x+\frac{13}{2}\), 當y=0時,x=\(\frac{13}{2}\times\frac{2}{3}=\frac{13}{3}\),故選\(\bbox[red,2pt]{(C)}\)。
解:
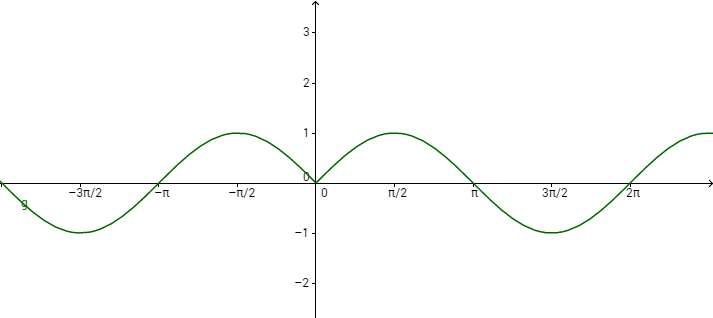
f(x)=sin|x|的圖形如上, x=0時,f'(x)不存在;當x=\(-\pi\)時,其斜率為正;當x=\(\pi\)時,其斜率為負;又\(f(x)=\sin{x}\Rightarrow f'(x)=\cos{x}\),故選\(\bbox[red,2pt]{(B)}\)。
解:



























沒有留言:
張貼留言