解：$$a>0且b<0\Rightarrow ab<0且b-a<0\Rightarrow (ab,b-a)在第三象限，故選\bbox[red,2pt]{(C)}。$$
解：$$\overrightarrow{BC}=\overrightarrow{AD}\Rightarrow (-5,0)=(x-5,y-2)\Rightarrow x=0,y=2，故選\bbox[red,2pt]{(B)}。$$
解：$$\sqrt { \sin ^{ 2 }{ 15°+\sin ^{ 2 }{ 75° } } } =\sqrt { \sin ^{ 2 }{ 15°+\cos ^{ 2 }{ 15° } } } =\sqrt { 1 } =1，故選\bbox[red,2pt]{(D)}。$$
解：
大角對大邊，所以c>b>a；因此\(\sec{47^\circ}=\frac{c}{a}>\frac{b}{a}=\tan{47^\circ}\)，故選\(\bbox[red,2pt]{(A)}\)。
解：由餘弦定理可知: \(b^2=a^2+c^2-2ac\cos{120^\circ}\Rightarrow b^2=36+c^2+6c \Rightarrow b^2-{(c+3)}^2=27\Rightarrow \)(b+c+3)(b-c-3)=27，可知b-c-3>0，即b-c>3；
又兩邊之和大於第三邊，因此a+c>b, 6>b-c；故選\(\bbox[red,2pt]{(B)}\)。
\Rightarrow k=1，故選\bbox[red,2pt]{(D)}。$$
解：$$x=\cos{20^\circ}代入多項式\Rightarrow 4\cos^3{20^\circ}- 3\cos{20^\circ}= \cos{60^\circ}=\frac{1}{2}，故選\bbox[red,2pt]{(B)}。$$
解：$$-\sqrt { 3 } +i=2\left( \frac { -\sqrt { 3 } }{ 2 } +\frac { 1 }{ 2 } i \right) =2\left( \cos { \frac { 5\pi }{ 6 } } +i\sin { \frac { 5\pi }{ 6 } } \right) \\ \Rightarrow arg\left( -\sqrt { 3 } +i \right) =\frac { 5\pi }{ 6 } ，故選\bbox[red,2pt]{(B)}。$$
解：$${ \left( \cos { \frac { \pi }{ 12 } } +i\sin { \frac { \pi }{ 12 } } \right) }^{ 10 }=\cos { \frac { 10\pi }{ 12 } } +i\sin { \frac { 10\pi }{ 12 } } =\cos { \frac { 5\pi }{ 6 } } +i\sin { \frac { 5\pi }{ 6 } } =\frac { -\sqrt { 3 } }{ 2 } +i\frac { 1 }{ 2 } \\ \Rightarrow a=\frac { -\sqrt { 3 } }{ 2 } ,b=\frac { 1 }{ 2 } \Rightarrow b-\sqrt { 3 } a=\frac { 1 }{ 2 } +\frac { 3 }{ 2 } =2，故選\bbox[red,2pt]{(D)}。$$
解：$$\left| \begin{matrix} 2a & -3 & 4d \\ 2b & -3 & 4d \\ -10c & 15 & -20f \end{matrix} \right| =-24\left| \begin{matrix} a & 1 & d \\ b & 1 & d \\ -5c & -5 & -5f \end{matrix} \right| =120\left| \begin{matrix} a & 1 & d \\ b & 1 & d \\ c & 5 & f \end{matrix} \right| =120\times 2=240\\，故選\bbox[red,2pt]{(C)}。$$
解：$$\tan { \frac { \pi }{ 6 } } =\frac { 1 }{ \sqrt { 3 } } =\frac { a }{ b } \Rightarrow a:b=1:\sqrt { 3 } ，故選\bbox[red,2pt]{(C)}。$$
解：沒有通過第一象限表示x截距與y截距皆為負值，即$$\begin{cases} -\frac { a+1 }{ 2 } \le 0 \\ \frac { a+1 }{ 3a-1 } \le 0 \end{cases}\Rightarrow \begin{cases} a\ge -1 \\ -1\le a\le \frac { 1 }{ 3 } \end{cases}，故選\bbox[red,2pt]{(B)}。$$
解：$$f\left( x \right) =4\left| x+1 \right| +3\left| 2x-1 \right| =\begin{cases} 4\left( x+1 \right) +3\left( 2x-1 \right) & x\ge \frac { 1 }{ 2 } \\ 4\left( x+1 \right) -3\left( 2x-1 \right) & -1\le x\le \frac { 1 }{ 2 } \\ -4\left( x+1 \right) -3\left( 2x-1 \right) & x\le -1 \end{cases}\\=\begin{cases} 10x+1 & x\ge \frac { 1 }{ 2 } \\ -2x+7 & -1\le x\le \frac { 1 }{ 2 } \\ -10x-1 & x\le -1 \end{cases}\Rightarrow x=\frac { 1 }{ 2 } 有最值6，故選\bbox[red,2pt]{(C)}。$$
$$2\ge x\ge -5\Rightarrow x+5\ge 2-x\Rightarrow 3x\ge -3\Rightarrow x\ge -1\Rightarrow 2\ge x\ge -1，故選\bbox[red,2pt]{(A)}。$$
解：圓方程式: \({(x+1)}^2+{(y-2)}^2=3^2\)，圓心坐標=(-1,2)；斜率1/2的直線方程式為2y=x+a，圓心代入可得 4=-1+a\(\Rightarrow a=5，故選\bbox[red,2pt]{(A)}\)。
解：拋物線為(x-2)(x+1)=\(x^2-x-2 \Rightarrow \)a=-1, b=-2，a+b=-3，故選\(\bbox[red,2pt]{(D)}\)。
解：過原點的直線方程式: y=mx代入橢圓只有一個解，即$${ \left( x-3 \right) }^{ 2 }+\frac { { m }^{ 2 }{ x }^{ 2 } }{ 4 } =1\Rightarrow \left( 4+{ m }^{ 2 } \right) { x }^{ 2 }-24x+32=0的判別式=0\\ \Rightarrow { 24 }^{ 2 }-4\times 32\times \left( 4+{ m }^{ 2 } \right) =0\Rightarrow 4+{ m }^{ 2 }=\frac { { 24 }^{ 2 } }{ 4\times 32 } =\frac { 9 }{ 2 } \Rightarrow { m }^{ 2 }=\frac { 1 }{ 2 } \\ \Rightarrow m=\pm \frac { 1 }{ \sqrt { 2 } } 故選\bbox[red,2pt]{(A)}。$$
解：$$\lim _{ h\rightarrow 0 }{ \frac { f\left( 3+h \right) -f\left( 3 \right) }{ h } } =f^{ ' }\left( 3 \right) =6\times 3+2=20，故選\bbox[red,2pt]{(C)}。$$
解：$$f\left( x \right) ={ x }^{ 3 }-2x\Rightarrow f'\left( x \right) ={ 3x }^{ 2 }-2\Rightarrow f''\left( x \right) =6x\Rightarrow f''\left( 1 \right) =6，故選\bbox[red,2pt]{(D)}。$$
解：$$\int _{ 1 }^{ 27 }{ \frac { 1 }{ \sqrt [ 3 ]{ x } } } dx=\int _{ 1 }^{ 27 }{ { { x }^{ -\frac { 1 }{ 3 } } } } dx=\left. \left( \frac { 3 }{ 2 } { x }^{ \frac { 2 }{ 3 } } \right) \right| _{ 1 }^{ 27 }=\left( \frac { 3 }{ 2 } \times { 27 }^{ \frac { 2 }{ 3 } } \right) -\left( \frac { 3 }{ 2 } \right) \\ =\frac { 27 }{ 2 } -\frac { 3 }{ 2 } =\frac { 24 }{ 2 } =12，故選\bbox[red,2pt]{(D)}。$$
解：$$\int _{ 0 }^{ 2 }{ x(2-x) } dx=\int _{ 0 }^{ 2 }{ 2x-{ x }^{ 2 } } dx=\left. \left( { x }^{ 2 }-\frac { 1 }{ 3 } { x }^{ 3 } \right) \right| _{ 0 }^{ 2 }=\left( 4-\frac { 8 }{ 3 } \right) -0=\frac { 4 }{ 3 } \\，故選\bbox[red,2pt]{(A)}。$$
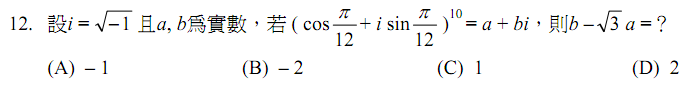
沒有留言:
張貼留言